
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 為等邊三角形,且平面
為等邊三角形,且平面![]() 平面
平面![]() .
.![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,過點
的中點,過點![]() ,
,![]() ,
,![]() 的平面交
的平面交![]() 于
于![]() .
.
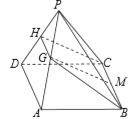
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
【題目】如圖程序框圖的算法思路源于數學名著《幾何原本》中的“輾轉相除法”,執行該程序框圖(圖中“m MOD n”表示m除以n的余數),若輸入的m,n分別為495,135,則輸出的m=( )
A.0
B.5
C.45
D.90
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,且當
上的偶函數,且當![]() 時,
時, ![]() .現已畫出函數
.現已畫出函數![]() 在
在![]() 軸左側的圖象,如圖所示,并根據圖象:
軸左側的圖象,如圖所示,并根據圖象:

(1)直接寫出函數![]() ,
, ![]() 的增區間;
的增區間;
(2)寫出函數![]() ,
, ![]() 的解析式;
的解析式;
(3)若函數![]() ,
, ![]() ,求函數
,求函數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若D′是平面α外一點,則下列命題正確的是( )
A.過D′只能作一條直線與平面α相交
B.過D′可作無數條直線與平面α垂直
C.過D′只能作一條直線與平面α平行
D.過D′可作無數條直線與平面α平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:萬元)的影響。對近六年的年宣傳費
(單位:萬元)的影響。對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() 的數據作了初步統計,得到如下數據:
的數據作了初步統計,得到如下數據:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣傳費 | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
經電腦擬,發現年宣傳費![]() (萬元)與年銷售量
(萬元)與年銷售量![]() (噸)之間近似滿足關系式
(噸)之間近似滿足關系式![]() 即
即![]() 。對上述數據作了初步處理,得到相關的值如下表:
。對上述數據作了初步處理,得到相關的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)規定當產品的年銷售量![]() (噸)與年宣傳費
(噸)與年宣傳費![]() (萬元)的比值在區間
(萬元)的比值在區間![]() 內時認為該年效益良好。現從這6年中任選2年,記其中選到效益良好年的數量為
內時認為該年效益良好。現從這6年中任選2年,記其中選到效益良好年的數量為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和期望。(其中
的分布列和期望。(其中![]() 為自然對數的底數,
為自然對數的底數, ![]() )
)
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以原點
),以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,若點
上一點,若點![]() 到曲線
到曲線![]() 的最小距離為
的最小距離為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】各項均為正數的數列{bn}的前n項和為Sn , 且對任意正整數n,都有2Sn=bn(bn+1).
(1)求數列{bn}的通項公式;
(2)如果等比數列{an}共有2015項,其首項與公比均為2,在數列{an}的每相鄰兩項ak與ak+1之間插入k個(﹣1)kbk(k∈N*)后,得到一個新的數列{cn}.求數列{cn}中所有項的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,求實數λ的范圍.
成立,求實數λ的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線x﹣9y﹣8=0與曲線C:y=x3﹣px2+3x相交于A,B,且曲線C在A,B處的切線平行,則實數p的值為( )
A.4
B.4或﹣3
C.﹣3或﹣1
D.﹣3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設D是函數y=f(x)定義域內的一個區間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com