
【題目】已知函數![]() ,其中
,其中![]() ,
, ![]() 是自然對數的底數.
是自然對數的底數.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)求函數![]() 的單調減區間;
的單調減區間;
(3)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)當
(2)當![]() 時,
時, ![]() 無單調減區間;當
無單調減區間;當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() ;當
;當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() .(3)
.(3)![]()
【解析】試題分析:(1)先對函數解析式進行求導,再借助導數的幾何意義求出切線的斜率,運用點斜式求出切線方程;(2)先對函數的解析式進行求導,然后借助導函數的值的符號與函數單調性之間的關系進行分類分析探求;(3)先不等式![]() 進行等價轉化,然后運用導數知識及分類整合的數學思想探求函數的極值與最值,進而分析推證不等式的成立求出參數的取值范圍。
進行等價轉化,然后運用導數知識及分類整合的數學思想探求函數的極值與最值,進而分析推證不等式的成立求出參數的取值范圍。
解:(1)因為![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() .
.
所以切線方程為![]() .
.
(2) 因為![]() ,
,
當![]() 時,
時, ![]() ,所以
,所以![]() 無單調減區間.
無單調減區間.
當![]() 即
即![]() 時,列表如下:
時,列表如下:

所以![]() 的單調減區間是
的單調減區間是![]() .
.
當![]() 即
即![]() 時,
時, ![]() ,列表如下:
,列表如下:
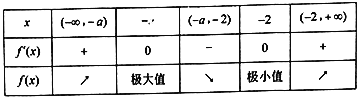
所以![]() 的單調減區間是
的單調減區間是![]() .
.
綜上,當![]() 時,
時, ![]() 無單調減區間;
無單調減區間;
當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() ;
;
當![]() 時,
時, ![]() 的單調減區間是
的單調減區間是![]() .
.
(3) ![]() .
.
當![]() 時,由(2)可得,
時,由(2)可得, ![]() 為
為![]() 上單調增函數,
上單調增函數,
所以![]() 在區間
在區間![]() 上的最大值
上的最大值![]() ,符合題意.
,符合題意.
當![]() 時,由(2)可得,要使
時,由(2)可得,要使![]() 在區間
在區間![]() 上恒成立,
上恒成立,
只需![]() ,
, ![]() ,解得
,解得![]() .
.
當![]() 時,可得
時,可得![]() ,
, ![]() .
.
設![]() ,則
,則![]() ,列表如下:
,列表如下:

所以![]() ,可得
,可得![]() 恒成立,所以
恒成立,所以![]() .
.
當![]() 時,可得
時,可得![]() ,無解.
,無解.
綜上, ![]() 的取值范圍是
的取值范圍是![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
【題目】在一個圓形波浪實驗水池的中心有三個振動源,假如不計其它因素,在t秒內,它們引發的水面波動可分別由函數 ![]() 和
和 ![]() 描述,如果兩個振動源同時啟動,則水面波動由兩個函數的和表達,在某一時刻使這三個振動源同時開始工作,那么,原本平靜的水面將呈現的狀態是( )
描述,如果兩個振動源同時啟動,則水面波動由兩個函數的和表達,在某一時刻使這三個振動源同時開始工作,那么,原本平靜的水面將呈現的狀態是( )
A.仍保持平靜
B.不斷波動
C.周期性保持平靜
D.周期性保持波動
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體ABCD﹣A1B1C1D1 , O是底ABCD對角線的交點.求證: 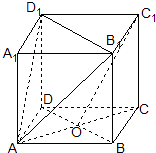
(1)C1O∥面AB1D1;
(2)面BDC1∥面AB1D1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
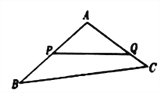
【題目】如圖,某生態園將一塊三角形地![]() 的一角
的一角![]() 開辟為水果園,已知角
開辟為水果園,已知角![]() 為
為![]() ,
, ![]() 的長度均大于200米,現在邊界
的長度均大于200米,現在邊界![]() 處建圍墻,在
處建圍墻,在![]() 處圍竹籬笆.
處圍竹籬笆.
(1)若圍墻![]() 、
、![]() 總長度為200米,如何可使得三角形地塊
總長度為200米,如何可使得三角形地塊![]() 面積最大?
面積最大?
(2)已知竹籬笆長為![]() 米,
米, ![]() 段圍墻高1米,
段圍墻高1米, ![]() 段圍墻高2米,造價均為每平方米100元,求圍墻總造價的取值范圍.
段圍墻高2米,造價均為每平方米100元,求圍墻總造價的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(n)=n2cos(nπ),且an=f(n)+f(n+1),則a1+a2+a3+…+a100=( )
A.0
B.﹣100
C.100
D.10200
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取一個年份,對西安市該年4月份的天氣情況進行統計,結果如下:
(Ⅰ)在4月份任取一天,估計西安市在該天不下雨的概率;
(Ⅱ)西安市某學校擬從4月份的一個晴天開始舉行連續2天的運動會,估計運動會期間不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天氣 | 晴 | 雨 | 陰 | 陰 | 陰 | 雨 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天氣 | 晴 | 陰 | 雨 | 陰 | 陰 | 晴 | 陰 | 晴 | 晴 | 晴 | 陰 | 晴 | 晴 | 晴 | 雨 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面四邊形ABCD中,AD=1,CD=2,AC= ![]() .
. 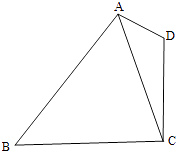
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com