
【題目】已知圓![]() 與橢圓
與橢圓![]() 相交于點M(0,1),N(0,-1),且橢圓的離心率為
相交于點M(0,1),N(0,-1),且橢圓的離心率為![]() .
.

(1)求![]() 的值和橢圓C的方程;
的值和橢圓C的方程;
(2)過點M的直線![]() 交圓O和橢圓C分別于A,B兩點.
交圓O和橢圓C分別于A,B兩點.
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②設直線NA的斜率為![]() ,直線NB的斜率為
,直線NB的斜率為![]() ,問:
,問:![]() 是否為定值? 如果是,求出定值;如果不是,說明理由.
是否為定值? 如果是,求出定值;如果不是,說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】狄利克雷是19世紀德國著名的數學家,他定義了一個“奇怪的函數” ,下列關于狄利克雷函數的敘述正確的有:______.
,下列關于狄利克雷函數的敘述正確的有:______.
①![]() 的定義域為
的定義域為![]() ,值域是
,值域是![]() ②
②![]() 具有奇偶性,且是偶函數
具有奇偶性,且是偶函數
③![]() 是周期函數,但它沒有最小正周期 ④對任意的
是周期函數,但它沒有最小正周期 ④對任意的![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中放有大小和形狀相同而顏色互不相同的小球若干個, 其中標號為0的小球1個, 標號為1的小球1個, 標號為2的小球2個, 從袋子中不放回地隨機抽取2個小球, 記第一次取出的小球標號為![]() ,第二次取出的小球標號為
,第二次取出的小球標號為![]() .
.
(1) 記事件![]() 表示“
表示“![]() ”, 求事件
”, 求事件![]() 的概率;
的概率;
(2) 在區間![]() 內任取2個實數
內任取2個實數![]() , 記
, 記![]() 的最大值為
的最大值為![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,滿足:
中,滿足:![]() ,M是
,M是![]() 的中點.
的中點.
(1)若![]() ,求向量
,求向量![]() 與向量
與向量![]() 的夾角的余弦值;
的夾角的余弦值;
(2)若O是線段![]() 上任意一點,且
上任意一點,且![]() ,求
,求![]() 的最小值:
的最小值:
(3)若點P是![]() 內一點,且
內一點,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,底面ABC為正三角形,
中,底面ABC為正三角形,![]() 底面ABC,
底面ABC,![]() ,點
,點![]() 在線段
在線段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)請指出點![]() 的位置,并給出證明;
的位置,并給出證明;
(2)若![]() ,求
,求![]() 與平面ABE夾角的正弦值.
與平面ABE夾角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
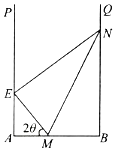
【題目】某地擬在一個U形水面PABQ(∠A=∠B=90°)上修一條堤壩(E在AP上,N在BQ上),圍出一個封閉區域EABN,用以種植水生植物.為了美觀起見,決定從AB上點M處分別向點E,N拉2條分隔線ME,MN,將所圍區域分成3個部分(如圖),每部分種植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,設所拉分隔線總長度為l.
(1)設∠AME=2θ,求用θ表示的l函數表達式,并寫出定義域;
(2)求l的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 是函數
是函數![]()
![]() 圖象上的任意兩點,且角
圖象上的任意兩點,且角![]() 的終邊經過點
的終邊經過點![]() ,若
,若![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 內有兩個不同的解,求實數
內有兩個不同的解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com