【題目】設函數(shù)
，其中
，
（1）若
，且
是
的極大值點，求的取值范圍；
（2）當
，
時，方程
有唯一實數(shù)根，求正數(shù)
的值.
【答案】（1）
；（2）
.
【解析】
（1）由
，知
，
，由
，得
，故
．由此能求出
的取值范圍．
（2）由方程
有唯一實數(shù)解，知
有唯一實數(shù)解，設
，則
，令
，得
．由此入手能夠推導出正數(shù)
的值．
解：（1）∵
，其中，
∴，
，由
，得，
∴
.
①若
，由，得
，
當
時，
，此時
單調遞增；
當
時，
，此時單調遞減，所以是的極大值點.
②若
，則，得，或
，∵是的極大值點，
∴
，解得
.
綜合①②，得的取值范圍是.
（2）∵方程
中唯一實數(shù)解，∴
有唯一實數(shù)解，
設
，則
，
令
，得.∵
，∴
，
方程有兩異號根
，設
，∵，∴
應舍去.
當
時，
，
在
上單調遞減，
當
時，
，在
上單調遞增，
當
時，
，取最小值
.
∵
有唯一解，∴
，
則
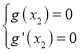，即
，∴
，
∵，∴
（*），
設函數(shù)
，∵當時，
是增函數(shù)，
∴
至多有一解，∵
，∴方程（*）的解為
，
代入方程組解得.
挑戰(zhàn)100單元檢測試卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系
中，如圖，已知橢圓E：
的左、右頂點分別為
、
，上、下頂點分別為
、
．設直線
傾斜角的余弦值為
，圓
與以線段
為直徑的圓關于直線對稱．
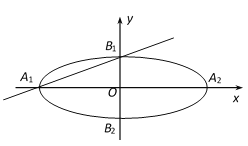
（1）求橢圓E的離心率；
（2）判斷直線與圓的位置關系，并說明理由；
（3）若圓的面積為
，求圓的方程．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
．
（1）設θ∈[0，π]，且f（θ）
1，求θ的值；
（2）在△ABC中，AB＝1，f（C）1，且△ABC的面積為
，求sinA+sinB的值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）＝|2x+3|+|2x﹣1|．
（1）求不等式f（x）≤6的解集；
（2）若關于x的不等式f（x）＜|m﹣1|的解集非空，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
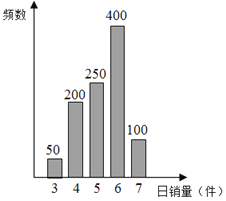
【題目】某公司銷售部隨機抽取了1000名銷售員1天的銷售記錄，經(jīng)統(tǒng)計，其柱狀圖如圖．
該公司給出了兩種日薪方案．
方案1：沒有底薪，每銷售一件薪資20元；
方案2：底薪90元，每日前5件的銷售量沒有獎勵，超過5件的部分每件獎勵20元．
（1）分別求出兩種日薪方案中日工資y（單位：元）與銷售件數(shù)n的函數(shù)關系式；
（2）若將頻率視為概率，回答下列問題：
（Ⅰ）根據(jù)柱狀圖，試分別估計兩種方案的日薪X（單位：元）的數(shù)學期望及方差；
（Ⅱ）如果你要應聘該公司的銷售員，結合（Ⅰ）中的數(shù)據(jù)，根據(jù)統(tǒng)計學的思想，分析選擇哪種薪資方案比較合適，并說明你的理由．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
