
【題目】已知函數![]()
(Ⅰ)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)當![]() 時,求
時,求![]() 的零點個數;
的零點個數;
(Ⅲ)若函數![]() 在
在![]() 上是增函數,求證:
上是增函數,求證:![]() .
.
【答案】(Ⅰ)![]() .(Ⅱ)見解析.(Ⅲ)見解析.
.(Ⅱ)見解析.(Ⅲ)見解析.
【解析】
(Ⅰ)由題意,求得![]() ,求得
,求得![]() ,得到切線的斜率,利用點斜式方程,即可得到切線的方程;
,得到切線的斜率,利用點斜式方程,即可得到切線的方程;
(Ⅱ)由![]() ,得到
,得到![]() 在
在![]() 上是增函數,進而得到
上是增函數,進而得到![]() ,再根據零點的存在定理,即可求解.
,再根據零點的存在定理,即可求解.
(Ⅲ)由題意得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,設
上恒成立,設![]() ,利用導數得到函數
,利用導數得到函數![]() 的單調性與最值,即可求解.
的單調性與最值,即可求解.
解:(Ⅰ)![]()
![]() 則:
則:![]() ,又
,又![]()
所以,所求切線方程為![]() ,即
,即![]() .
.
(Ⅱ)因為![]() ,
,
所以![]() 在
在![]() 上是增函數,
上是增函數,
則![]() ,
,
所以![]() 在
在![]() 上是增函數,
上是增函數,
又![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有唯一零點,且零點在
上有唯一零點,且零點在![]() 上.
上.
(Ⅲ)由題意,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() 恒成立,
恒成立,
設![]()
所以![]() ,
,
由(Ⅱ)可知,![]() ,使
,使![]() ,
,
所以,當![]() 時,
時,![]() ,當
,當![]() 時
時![]()
由此,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
所以,![]()
又因為![]() ,
,
所以![]()
從而![]() ,
,
所以![]() .
.
又因為,![]() ,
,
![]() ,
,
所以![]() .
.
由于![]() 在
在![]() 上是增函數,
上是增函數,
所以![]() ,
,
故![]() .
.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg), 其頻率分布直方圖如下:

(1)記A表示事件“舊養殖法的箱產量低于50 kg”,估計A的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:
箱產量<50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對這兩種養殖方法的優劣進行比較.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四面體ABCD中,![]() 與
與![]() 都是邊長為8的正三角形,點O是線段BC的中點.
都是邊長為8的正三角形,點O是線段BC的中點.
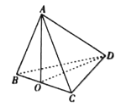
(1)證明:![]() .
.
(2)若![]() 為銳角,且四面體ABCD的體積為
為銳角,且四面體ABCD的體積為![]() 求側面ACD的面積.
求側面ACD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產基地有五臺機器,現有五項工作待完成,每臺機器完成每項工作后獲得的效益值如表所示.若每臺機器只完成一項工作,且完成五項工作后獲得的效益值總和最大,則下列敘述錯誤的的是_____________.
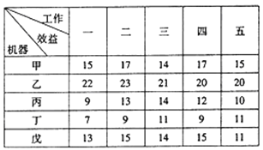
①甲只能承擔第四項工作
②乙不能承擔第二項工作
③丙可以不承擔第三項工作
④丁可以承擔第三項工作
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)直接寫出![]() 的零點;
的零點;
(2)在坐標系中,畫出![]() 的示意圖(注意要畫在答題紙上)
的示意圖(注意要畫在答題紙上)
(3)根據圖象討論關于![]() 的方程
的方程![]() 的解的個數:
的解的個數:
(4)若方程![]() ,有四個不同的根
,有四個不同的根![]() 、
、![]() 、
、![]() 、
、![]() 直接寫出這四個根的和;
直接寫出這四個根的和;
(5)若函數![]() 在區間
在區間![]() 上既有最大值又有最小值,直接寫出a的取值范圍.
上既有最大值又有最小值,直接寫出a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在含有![]() 個元素的集合
個元素的集合![]() 中,若這
中,若這![]() 個元素的一個排列(
個元素的一個排列(![]() ,
,![]() ,…,
,…,![]() )滿足
)滿足![]() ,則稱這個排列為集合
,則稱這個排列為集合![]() 的一個錯位排列(例如:對于集合
的一個錯位排列(例如:對于集合![]() ,排列
,排列![]() 是
是![]() 的一個錯位排列;排列
的一個錯位排列;排列![]() 不是
不是![]() 的一個錯位排列).記集合
的一個錯位排列).記集合![]() 的所有錯位排列的個數為
的所有錯位排列的個數為![]() .
.
(1)直接寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)當![]() 時,試用
時,試用![]() ,
,![]() 表示
表示![]() ,并說明理由;
,并說明理由;
(3)試用數學歸納法證明:![]() 為奇數.
為奇數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限x和所支出的維修費用y(萬元)有如下的統計資料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
維修費用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由資料知y對x呈線性相關關系.
(1)請畫出上表數據的散點圖;
(2)請根據最小二乘法求出線性回歸方程![]() 的回歸系數a,b;
的回歸系數a,b;
(3)估計使用年限為10年時,維修費用是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線![]() 和
和![]() 是異面直線,
是異面直線,![]() 在平面
在平面![]() 內,
內,![]() 在平面
在平面![]() 內,
內,![]() 是平面
是平面![]() 與平面
與平面![]() 的交線,則下列命題正確的是( )
的交線,則下列命題正確的是( )
A. ![]() 與
與![]() 都不相交 B.
都不相交 B. ![]() 與
與![]() 都相交
都相交
C. ![]() 至多與
至多與![]() 中的一條相交 D.
中的一條相交 D. ![]() 至少與
至少與![]() 中的一條相交
中的一條相交
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com