
【題目】已知函數![]() ,
, ![]() .
.
(1)若函數![]() 在
在![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在整數![]() ,
, ![]() ,使得
,使得![]() 的解集恰好是
的解集恰好是![]() ,若存在,求出
,若存在,求出![]() ,
, ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】試題分析:(1)根據二次函數圖像確定對稱軸一定在區間![]() 外,再根據左右位置對于單調性確定函數值的正負,解不等式可得實數
外,再根據左右位置對于單調性確定函數值的正負,解不等式可得實數![]() 的取值范圍;(2)根據對稱軸與定義區間位置關系討論函數值對應關系,消去m得關于a,b關系式,根據整數條件確定有限解,最后驗證確定滿足條件的解
的取值范圍;(2)根據對稱軸與定義區間位置關系討論函數值對應關系,消去m得關于a,b關系式,根據整數條件確定有限解,最后驗證確定滿足條件的解
試題解析:(1)令![]() ,則
,則![]() .
.
當![]() ,即
,即![]() 時,
時, ![]() 恒成立,
恒成立,
所以![]() .
.
因為![]() 在
在![]() 上是減函數,所以
上是減函數,所以![]() ,解得
,解得![]() ,
,
所以![]() .
.
由![]() ,解得
,解得![]() 或
或![]() ,
,
當![]() 時,
時, ![]() 的圖象對稱軸
的圖象對稱軸![]() ,且方程
,且方程![]() 的兩根均為正,
的兩根均為正,
此時![]() 在
在![]() 為減函數,所以
為減函數,所以![]() 符合條件.
符合條件.
當![]() 時,
時, ![]() 的圖象對稱軸
的圖象對稱軸![]() ,且方程
,且方程![]() 的根一正一負,
的根一正一負,
要使![]() 在
在![]() 單調遞減,則
單調遞減,則![]() ,解得
,解得![]() .
.
綜上可得,實數![]() 的取值范圍為
的取值范圍為![]() .
.
(2)假設存在整數![]() 、
、![]() ,使
,使![]() 的解集恰好是
的解集恰好是![]() ,則
,則
①若函數![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ,
, ![]() 且
且![]() ,
,
即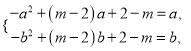
作差得到![]() ,代回得到
,代回得到![]() ,即
,即![]() ,
,
由于![]() 、
、![]() 均為整數,
均為整數,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,經檢驗均不滿足要求;
,經檢驗均不滿足要求;
②若函數![]() 在
在![]() 上單調遞減,則
上單調遞減,則![]() ,
, ![]() 且
且![]() ,
,
即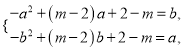
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,
,
由于![]() 、
、![]() 均為整數,
均為整數,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,經檢驗均不滿足要求;
,經檢驗均不滿足要求;
③若函數![]() 在
在![]() 上不單調,則
上不單調,則![]() ,
, ![]() ,且
,且![]() ,
,
即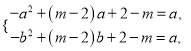
作差得到![]() ,代回得到
,代回得到![]() ,即
,即![]() ,由于
,由于![]() ,
, ![]() 均為整數,
均為整數,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,經檢驗均滿足要求;
,經檢驗均滿足要求;
綜上:符合要求的整數![]() 、
、![]() 是
是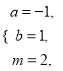 或
或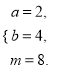 .
.


科目:高中數學 來源: 題型:
【題目】定義在R上的函數y=f(x)對任意的x、y∈R,滿足條件:f(x+y)=f(x)+f(y)﹣1,且當x>0時,f(x)>1.
(1)求f(0)的值;
(2)證明:函數f(x)是R上的單調增函數;
(3)解關于t的不等式f(2t2﹣t)<1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式﹣2<|x﹣1|﹣|x+2|<0的解集為M,a,b∈M. (Ⅰ)證明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(Ⅱ)比較|1﹣4ab|與2|a﹣b|的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 中,底面
中,底面![]() 是邊長為1的正方形,側棱
是邊長為1的正方形,側棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是側棱
是側棱![]() 上的動點.
上的動點.
(1)求四棱錐![]() 的表面積;
的表面積;
(2)是否在棱![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 平面
平面![]() ;若存在,指出點
;若存在,指出點![]() 的位置,并證明;若不存在,請說明理由.
的位置,并證明;若不存在,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,當
,當![]() 時,恒有
時,恒有![]() .當
.當![]() 時,
時, ![]() .
.
(Ⅰ)求證: ![]() 是奇函數;
是奇函數;
(Ⅱ)若![]() ,試求
,試求![]() 在區間
在區間![]() 上的最值;
上的最值;
(Ⅲ)是否存在![]() ,使
,使![]() 對于任意
對于任意![]() 恒成立?若存在,求出實數
恒成立?若存在,求出實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在南北方向有一條公路,一半徑為100m的圓形廣場(圓心為O)與此公路一邊所在直線l相切于點A.點P為北半圓弧(弧APB)上的一點,過P作直線l的垂線,垂足為Q.計劃在△PAQ內(圖中陰影部分)進行綠化.設△PAQ的面積為S(單位:m2). 
(1)設∠BOP=α(rad),將S表示為α的函數;
(2)確定點P的位置,使綠化面積最大,并求出最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的奇函數,且當x>0時,f(x)=log2x,g(x)=2log2(2x+a),a∈R
(1)求函數f(x)的解析式;
(2)若對任意x∈[1,4],f(4x)≤g(x),求實數a的取值范圍;
(3)設a>﹣2,求函數h(x)=g(x)﹣f(x),x∈[1,2]的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com