
【題目】已知![]() ,
,![]()
(1)求![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若![]() ,
,![]() 在其公共點
在其公共點![]() 處切線相同,求實數a的值;
處切線相同,求實數a的值;
(3)記![]() ,若函數
,若函數![]() 存在兩個零點,求實數a的取值范圍.
存在兩個零點,求實數a的取值范圍.
【答案】(1)函數的單調減區(qū)間為:![]() ;增區(qū)間為:
;增區(qū)間為:![]() (2)
(2)![]() (3)a>e
(3)a>e
【解析】
(1)根據![]() ,求導,由
,求導,由![]() 求減區(qū)間,由
求減區(qū)間,由![]() 求增區(qū)間.
求增區(qū)間.
(2)由![]() ,求導
,求導![]() ,根據
,根據![]() ,
,![]() 在其公共點
在其公共點![]() 處切線相同,由
處切線相同,由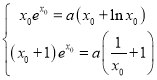 求解.
求解.
(3)易得![]() ,x>0.,求導
,x>0.,求導![]() ,令
,令![]() 得,
得,![]() ,然后分a≤0和a>0兩種情況討論求解.
,然后分a≤0和a>0兩種情況討論求解.
(1)因為![]() ,
,
所以![]() ,
,
得x=-1,
當x<-1時,![]() ;當x>-1時,
;當x>-1時,![]() .
.
所以函數的單調減區(qū)間為:![]() ;增區(qū)間為:
;增區(qū)間為:![]() .
.
(2)由![]() ,
,![]() .
.
因為點![]() 為函數
為函數![]() 的公共點,且函數
的公共點,且函數![]() 在點P處的切線相同,
在點P處的切線相同,
所以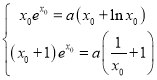 ,且
,且![]() .
.
所以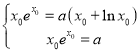 ,
,
即![]() ,
,
顯然a≠0,所以![]() .
.
設![]() ,由
,由![]() 得,
得,![]() 在
在![]() 上是單調增函數,
上是單調增函數,
又![]() ,所以
,所以![]() .
.
(3)由![]() 得,
得,![]() ,x>0.
,x>0.
則![]() ,
,
令![]() 得,
得,![]() .
.
設![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上是單調增函數.
上是單調增函數.
1°當a≤0時,由x>0得,![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上是單調增函數,至多1個零點,不符,舍去.
上是單調增函數,至多1個零點,不符,舍去.
2°當a>0時,因為![]() ,
,![]() ,
,
由零點存在性定理,![]() ,
,![]() 在
在![]() 上是單調增函數且連續(xù),
上是單調增函數且連續(xù),
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
因為![]() 存在兩個零點,
存在兩個零點,
所以![]() ,即
,即![]() ,從而
,從而![]() .
.
所以![]() .
.
因為![]() 在
在![]() 上是單調增函數,
上是單調增函數,
且![]() ,所以
,所以![]() ,
,
由(1)可知,![]() 在
在![]() 是單調遞增,
是單調遞增,
所以![]() .
.
又![]() ,
,![]() ,
,
而![]() ,易得
,易得![]() ,
,![]() ,
,
所以![]() ,
,
由零點存在性定理知,函數![]() 在
在![]() 上存在唯一一個零點,在
上存在唯一一個零點,在![]() 上存在唯一一個零點,
上存在唯一一個零點,
此時函數![]() 存在兩個零點.
存在兩個零點.
所以a>e.


科目:高中數學 來源: 題型:
【題目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 這三個條件中任選一個,補充在下面問題中,若問題中的
這三個條件中任選一個,補充在下面問題中,若問題中的![]() 存在,求出
存在,求出![]() 和數列
和數列![]() 的通項公式與前
的通項公式與前![]() 項和;若
項和;若![]() 不存在,請說明理由.
不存在,請說明理由.
設![]() 為各項均為正數的數列
為各項均為正數的數列![]() 的前
的前![]() 項和,滿足________,是否存在
項和,滿足________,是否存在![]() ,使得數列
,使得數列![]() 成為等差數列?
成為等差數列?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了對某種商品進行合理定價,需了解該商品的月銷售量![]() (單位:萬件)與月銷售單價
(單位:萬件)與月銷售單價![]() (單位:元/件)之間的關系,對近
(單位:元/件)之間的關系,對近![]() 個月的月銷售量
個月的月銷售量![]() 和月銷售單價
和月銷售單價![]()
![]() 數據進行了統(tǒng)計分析,得到一組檢測數據如表所示:
數據進行了統(tǒng)計分析,得到一組檢測數據如表所示:
月銷售單價 |
|
|
|
|
|
|
月銷售量 |
|
|
|
|
|
|
(1)若用線性回歸模型擬合![]() 與
與![]() 之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:
之間的關系,現有甲、乙、丙三位實習員工求得回歸直線方程分別為:![]() ,
,![]() 和
和![]() ,其中有且僅有一位實習員工的計算結果是正確的.請結合統(tǒng)計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
,其中有且僅有一位實習員工的計算結果是正確的.請結合統(tǒng)計學的相關知識,判斷哪位實習員工的計算結果是正確的,并說明理由;
(2)若用![]() 模型擬合
模型擬合![]() 與
與![]() 之間的關系,可得回歸方程為
之間的關系,可得回歸方程為![]() ,經計算該模型和(1)中正確的線性回歸模型的相關指數
,經計算該模型和(1)中正確的線性回歸模型的相關指數![]() 分別為
分別為![]() 和
和![]() ,請用
,請用![]() 說明哪個回歸模型的擬合效果更好;
說明哪個回歸模型的擬合效果更好;
(3)已知該商品的月銷售額為![]() (單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到
(單位:萬元),利用(2)中的結果回答問題:當月銷售單價為何值時,商品的月銷售額預報值最大?(精確到![]() )
)
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】斐波拉契數列,指的是這樣一個數列:1,1,2,3,5,8,13,21,…,在數學上,斐波拉契數列{an}定義如下:a1=a2=1,an=an﹣1+an﹣2(n≥3,n∈N),隨著n的增大,![]() 越來越逼近黃金分割
越來越逼近黃金分割![]() 0.618,故此數列也稱黃金分割數列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
0.618,故此數列也稱黃金分割數列,而以an+1、an為長和寬的長方形稱為“最美長方形”,已知某“最美長方形”的面積約為200平方厘米,則該長方形的長大約是( )
A.20厘米B.19厘米C.18厘米D.17厘米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣1)2﹣alnx(a<0).
(1)討論f(x)的單調性;
(2)若f(x)存在兩個極值點x1,x2(x1<x2),且關于x的方程f(x)=b(b∈R)恰有三個實數根x3,x4,x5(x3<x4<x5),求證:2(x2﹣x1)>x5﹣x3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由![]() 和
和![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() 是
是![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,將
,將![]() 和
和![]() 分別沿著
分別沿著![]() ,
,![]() 折起,使得
折起,使得![]() 與
與![]() 重合于點B,G為
重合于點B,G為![]() 的中點,如圖2.
的中點,如圖2.
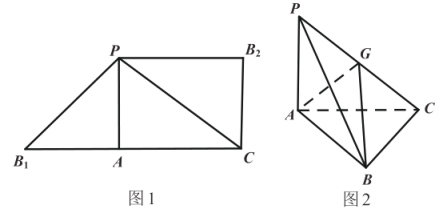
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求點C到平面
,求點C到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:![]() (
(![]() )的焦點為F,過F且斜率為1的直線與C交于A,B兩點,
)的焦點為F,過F且斜率為1的直線與C交于A,B兩點,![]() .
.
(1)求C的方程;
(2)過點![]() 的直線l交C于點M,N,點Q為
的直線l交C于點M,N,點Q為![]() 的中點,
的中點,![]() 軸交C于點R,且
軸交C于點R,且![]() ,證明:動點T在定直線上.
,證明:動點T在定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“紋樣”是中國藝術寶庫的瑰寶,“火紋”是常見的一種傳統(tǒng)紋樣,為了測算某火紋紋樣(如圖陰影部分所示)的面積,作一個邊長為3的正方形將其包含在內,并向該正方形內隨機投擲2000個點,己知恰有800個點落在陰影部分,據此可估計陰影部分的面積是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com