
【題目】已知一條曲線C在y軸右側,曲線C上任意一點到點![]() 的距離減去它到y軸的距離都等于1.
的距離減去它到y軸的距離都等于1.
(1)求曲線C的方程;
(2)直線![]() 與軌跡C交于A,B兩點,問:在x軸上是否存在定點
與軌跡C交于A,B兩點,問:在x軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與直線
關于x軸對稱而與直線![]() 的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)直接根據題意得到方程化簡得到答案.
(2)設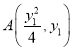 ,
,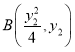 ,聯立方程,根據韋達定理得到根與系數關系,計算
,聯立方程,根據韋達定理得到根與系數關系,計算![]() ,化簡整理得到答案.
,化簡整理得到答案.
(1)設![]() 是曲線C上任意一點,那么點
是曲線C上任意一點,那么點![]() 滿足:
滿足:![]() ,
,
化簡得![]() ,又因為曲線C在y軸右側,故
,又因為曲線C在y軸右側,故![]() ,
,
所以曲線C方程為:![]() .
.
(2)在x軸上存在定點![]() 使得直線
使得直線![]() 與
與![]() 關于x軸對稱而與
關于x軸對稱而與![]() 位置無關.
位置無關.
理由如下:
設直線![]() 與曲線C的交點坐標為
與曲線C的交點坐標為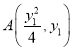 ,
,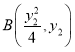 ,
,
由![]() ,消去x,整理得
,消去x,整理得![]() ,
,![]() ,
,
由韋達定理得![]() ,
,![]() ,.
,.
假設存在點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與
關于x軸對稱而與![]() 位置無關,
位置無關,
則![]() 對任意實數m恒成立,即
對任意實數m恒成立,即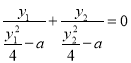 對任意實數m恒成立,
對任意實數m恒成立,
而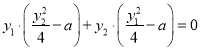 ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() .
.
故當![]() 對任意實數m,
對任意實數m,![]() ,
,
即在x軸上存在點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與
關于x軸對稱而與![]() 位置無關.
位置無關.


科目:高中數學 來源: 題型:
【題目】已知![]() 是定義域為
是定義域為![]() 的偶函數,對
的偶函數,對![]() ,有
,有![]() ,且當
,且當![]() 時,
時,![]() ,函數
,函數![]() .現給出以下命題:①
.現給出以下命題:①![]() 是周期函數;②
是周期函數;②![]() 的圖象關于直線
的圖象關于直線![]() 對稱;③當
對稱;③當![]() 時,
時,![]() 在
在![]() 內有一個零點;④當
內有一個零點;④當![]() 時,
時,![]() 在
在![]() 上至少有六個零.其中正確命題的序號為________.
上至少有六個零.其中正確命題的序號為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】請從下面三個條件中任選一個,補充在下面的橫線上,并解答.
①![]()
②![]()
③![]() 的面積為
的面積為![]()
在![]() 中,內角A,B,C所對的邊分別為a,b,c,已知b-c=2,cosA=
中,內角A,B,C所對的邊分別為a,b,c,已知b-c=2,cosA=![]() , .
, .
(1)求a;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點
的中點![]() 是由
是由![]() 繞直線
繞直線![]() 旋轉得到,連結
旋轉得到,連結![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() ?若存在,確定點
?若存在,確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對任意![]() ,給定區間
,給定區間![]() ,設函數
,設函數![]() 表示實數
表示實數![]() 與
與![]() 所屬的給定區間內唯一整數之差的絕對值.
所屬的給定區間內唯一整數之差的絕對值.
(1)當![]() 時,求出
時,求出![]() 的解析式;
的解析式;![]() 時,寫出絕對值符號表示的
時,寫出絕對值符號表示的![]() 解析式;
解析式;
(2)求![]() ,
,![]() ,判斷函數
,判斷函數![]() 的奇偶性,并證明你的結論;
的奇偶性,并證明你的結論;
(3)當![]() 時,求方程
時,求方程![]() 的實根.(要求說明理由,
的實根.(要求說明理由,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】采購經理指數(PMI)是衡量一個國家制造業的“體檢表”,是衡量制造業在生產新訂單、商品價格、存貨、雇員、訂單交貨、新出口訂單和進口等八個方面狀況的指數,下圖為2018年9月—2019年9月我國制造業的采購經理指數(單位:%).
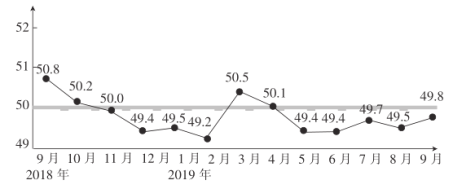
(1)求2019年前9個月我國制造業的采購經理指數的中位數及平均數(精確到0.1);
(2)從2019年4月—2019年9月這6個月任意選取2個月,求這兩個月至少有一個月采購經理指數與上個月相比有所回升的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】英國統計學家E.H.辛普森1951年提出了著名的辛普森悖論,下面這個案例可以讓我們感受到這個悖論.有甲乙兩名法官,他們都在民事庭和行政庭主持審理案件,他們審理的部分案件被提出上訴.記錄這些被上述案件的終審結果如下表所示(單位:件):
法官甲 | 法官乙 | ||||||
終審結果 | 民事庭 | 行政庭 | 合計 | 終審結果 | 民事庭 | 行政庭 | 合計 |
維持 | 29 | 100 | 129 | 維持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合計 | 32 | 118 | 150 | 合計 | 100 | 25 | 125 |
記甲法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為
,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,則下面說法正確的是
,則下面說法正確的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com