
【題目】請從下面三個條件中任選一個,補充在下面的橫線上,并解答.
①![]()
②![]()
③![]() 的面積為
的面積為![]()
在![]() 中,內角A,B,C所對的邊分別為a,b,c,已知b-c=2,cosA=
中,內角A,B,C所對的邊分別為a,b,c,已知b-c=2,cosA=![]() , .
, .
(1)求a;
(2)求![]() 的值.
的值.
【答案】(1)不論選哪種條件,a=8(2)![]()
【解析】
方案一:選擇條件①:(1)首先利用向量的加法以及向量的數量積可得![]() ,從而可求出
,從而可求出![]() 、
、![]() ,然后再利用余弦定理即可求解.
,然后再利用余弦定理即可求解.
(2)利用余弦定理可得![]() ,再利用同角三角函數的基本關系求出
,再利用同角三角函數的基本關系求出![]() ,由二倍角公式以及兩角和的余弦公式即可求解.
,由二倍角公式以及兩角和的余弦公式即可求解.
方案二:選擇條件②:(1)求出![]() 、
、![]() ,再利用余弦定理即可求解.
,再利用余弦定理即可求解.
(2)同方案一
方案三:選擇條件③:(1)利用同角三角函數的基本關系求出![]() ,再利用三角形的面積公式可得
,再利用三角形的面積公式可得![]() ,求出
,求出![]() 、
、![]() ,再利用余弦定理即可求解.
,再利用余弦定理即可求解.
(2)同方案一.
解:方案一:選擇條件①:
(1)![]()
![]()
∵![]()
∴bc=24
由![]() 解得
解得![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴a=8
(2)![]()
![]()
![]()
∴![]()
∴![]()
![]()
∴![]()
![]()
方案二:選擇條件②:
(1)由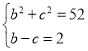 解得
解得![]() 或
或![]() (舍去)
(舍去)
∴![]()
∴a=8
(2)同方案一
方案三:選擇條件③:
(1)∵![]()
∴![]()
![]()
∴bc=24
由![]() 解得
解得![]() 或
或![]() (舍)
(舍)
∴![]()
∴a=8
(2)同方案一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的焦點為
)的焦點為![]() ,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線
,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓E的方程;
(2)過點F的直線l交橢圓E于M,N兩點,點P的坐標為![]() ,直線
,直線![]() 與x軸交于A點,直線
與x軸交于A點,直線![]() 與x軸交于B點,求證:
與x軸交于B點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】著名物理學家李政道說:“科學和藝術是不可分割的”.音樂中使用的樂音在高度上不是任意定的,它們是按照嚴格的數學方法確定的.我國明代的數學家、音樂理論家朱載填創立了十二平均律是第一個利用數學使音律公式化的人.十二平均律的生律法是精確規定八度的比例,把八度分成13個半音,使相鄰兩個半音之間的頻率比是常數,如下表所示,其中![]() 表示這些半音的頻率,它們滿足
表示這些半音的頻率,它們滿足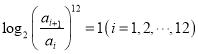 .若某一半音與
.若某一半音與![]() 的頻率之比為
的頻率之比為![]() ,則該半音為( )
,則該半音為( )
頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
半音 | C |
| D |
| E | F |
| G |
| A |
| B | C(八度) |
A.![]() B.GC.
B.GC.![]() D.A
D.A
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一條曲線C在y軸右側,曲線C上任意一點到點![]() 的距離減去它到y軸的距離都等于1.
的距離減去它到y軸的距離都等于1.
(1)求曲線C的方程;
(2)直線![]() 與軌跡C交于A,B兩點,問:在x軸上是否存在定點
與軌跡C交于A,B兩點,問:在x軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與直線
關于x軸對稱而與直線![]() 的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的右焦點為
)的右焦點為![]() ,左右頂點分別為
,左右頂點分別為![]() 、
、![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() (不與
(不與![]() 軸重合)交橢圓
軸重合)交橢圓![]() 于
于![]() 、
、![]() 點,直線
點,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() .
.
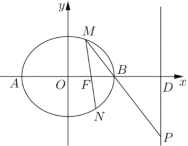
(1)求橢圓![]() 的方程;
的方程;
(2)若![]()
![]() ,求出點
,求出點![]() 的坐標;
的坐標;
(3)求證:![]() 、
、![]() 、
、![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 有兩個不同的零點
有兩個不同的零點![]() .
.
(ⅰ)求實數![]() 的取值范圍;
的取值范圍;
(ⅱ)求證:![]() .(其中
.(其中![]() 為
為![]() 的極小值點)
的極小值點)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com