
【題目】已知![]() 是定義域為
是定義域為![]() 的偶函數,對
的偶函數,對![]() ,有
,有![]() ,且當
,且當![]() 時,
時,![]() ,函數
,函數![]() .現給出以下命題:①
.現給出以下命題:①![]() 是周期函數;②
是周期函數;②![]() 的圖象關于直線
的圖象關于直線![]() 對稱;③當
對稱;③當![]() 時,
時,![]() 在
在![]() 內有一個零點;④當
內有一個零點;④當![]() 時,
時,![]() 在
在![]() 上至少有六個零.其中正確命題的序號為________.
上至少有六個零.其中正確命題的序號為________.
 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數學 來源: 題型:
【題目】設數列:A:a1,a2,…,an,B:b1,b2,…,bn.已知ai,bj∈{0,1}(i=1,2,…,n;j=1,2,…,n),定義n×n數表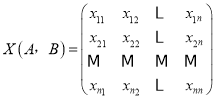 ,其中xij
,其中xij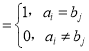 .
.
(1)若A:1,1,1,0,B:0,1,0,0,寫出X(A,B);
(2)若A,B是不同的數列,求證:n×n數表X(A,B)滿足“xij=xji(i=1,2,…,n;j=1,2,…,n;i![]() j)”的充分必要條件為“ak+bk=1(k=1,2,…,n)”;
j)”的充分必要條件為“ak+bk=1(k=1,2,…,n)”;
(3)若數列A與B中的1共有n個,求證:n×n數表X(A,B)中1的個數不大于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
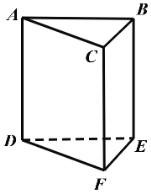
【題目】如圖,一顆棋子從三棱柱的一個項點沿棱移到相鄰的另一個頂點的概率均為![]() ,剛開始時,棋子在上底面點
,剛開始時,棋子在上底面點![]() 處,若移了
處,若移了![]() 次后,棋子落在上底面頂點的概率記為
次后,棋子落在上底面頂點的概率記為![]() .
.
(1)求![]() ,
,![]() 的值:
的值:
(2)求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為4的菱形,∠BAD=60°,對角線AC與BD相交于點O,四邊形ACFE為梯形,EF//AC,點E在平面ABCD上的射影為OA的中點,AE與平面ABCD所成角為45°.
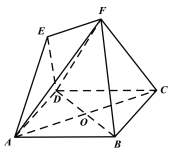
(Ⅰ)求證:BD⊥平面ACF;
(Ⅱ)求平面DEF與平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的焦點為
)的焦點為![]() ,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線
,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓E的方程;
(2)過點F的直線l交橢圓E于M,N兩點,點P的坐標為![]() ,直線
,直線![]() 與x軸交于A點,直線
與x軸交于A點,直線![]() 與x軸交于B點,求證:
與x軸交于B點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一條曲線C在y軸右側,曲線C上任意一點到點![]() 的距離減去它到y軸的距離都等于1.
的距離減去它到y軸的距離都等于1.
(1)求曲線C的方程;
(2)直線![]() 與軌跡C交于A,B兩點,問:在x軸上是否存在定點
與軌跡C交于A,B兩點,問:在x軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與直線
關于x軸對稱而與直線![]() 的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com