
【題目】采購經理指數(PMI)是衡量一個國家制造業的“體檢表”,是衡量制造業在生產新訂單、商品價格、存貨、雇員、訂單交貨、新出口訂單和進口等八個方面狀況的指數,下圖為2018年9月—2019年9月我國制造業的采購經理指數(單位:%).
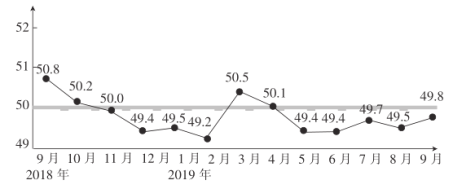
(1)求2019年前9個月我國制造業的采購經理指數的中位數及平均數(精確到0.1);
(2)從2019年4月—2019年9月這6個月任意選取2個月,求這兩個月至少有一個月采購經理指數與上個月相比有所回升的概率.
【答案】(1)中位數為![]() ,平均數為49.7;(2)
,平均數為49.7;(2)![]()
【解析】
(1)利用中位數和平均數的概念直接求解即可.
(2)利用列舉法列出所有可能滿足條件的結果,即可求出所求概率.
(1)2019年前9個月我國制造業的采購經理指數的中位數為![]() ,
,
平均數為![]() .
.
(2)從2019年4月—2019年9月這6個月任意選取2個月,結果總共有15種,
這6個月中采購經理指數與上個月相比有所回升的有7月9月,共2個,
所以從這6個月任意選取2個月,這兩個月至少有一個月采購經理指數與上個月相比有所回升的結果有(4月,7月),(5月,7月),(6月,7月),(8月,7月),(4月,9月),(5月,9月),(6月,9月),(8月,9月),(7月,9月),結果有9種,
所以所求概率![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的焦點為
)的焦點為![]() ,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線
,以原點O為圓心,橢圓E的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓E的方程;
(2)過點F的直線l交橢圓E于M,N兩點,點P的坐標為![]() ,直線
,直線![]() 與x軸交于A點,直線
與x軸交于A點,直線![]() 與x軸交于B點,求證:
與x軸交于B點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一條曲線C在y軸右側,曲線C上任意一點到點![]() 的距離減去它到y軸的距離都等于1.
的距離減去它到y軸的距離都等于1.
(1)求曲線C的方程;
(2)直線![]() 與軌跡C交于A,B兩點,問:在x軸上是否存在定點
與軌跡C交于A,B兩點,問:在x軸上是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 關于x軸對稱而與直線
關于x軸對稱而與直線![]() 的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
的位置無關,若存在,求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的右焦點為
)的右焦點為![]() ,左右頂點分別為
,左右頂點分別為![]() 、
、![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() (不與
(不與![]() 軸重合)交橢圓
軸重合)交橢圓![]() 于
于![]() 、
、![]() 點,直線
點,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() .
.
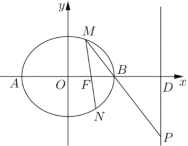
(1)求橢圓![]() 的方程;
的方程;
(2)若![]()
![]() ,求出點
,求出點![]() 的坐標;
的坐標;
(3)求證:![]() 、
、![]() 、
、![]() 三點共線.
三點共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的多面體ABCDEF滿足:正方形ABCD與正三角形FBC所在的兩個平面互相垂直,FB∥AE且FB=2EA.
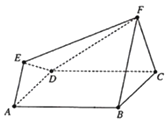
(1)證明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
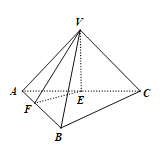
【題目】如圖,三棱錐![]() 的側棱長都相等,底面
的側棱長都相等,底面![]() 與側面
與側面![]() 都是以
都是以![]() 為斜邊的等腰直角三角形,
為斜邊的等腰直角三角形,![]() 為線段
為線段![]() 的中點,
的中點,![]() 為直線
為直線![]() 上的動點,若平面
上的動點,若平面![]() 與平面
與平面![]() 所成銳二面角的平面角為
所成銳二面角的平面角為![]() ,則
,則![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 是
是![]() 上一點.
上一點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 是
是![]() 分別關于兩坐標軸及坐標原點的對稱點,平行于
分別關于兩坐標軸及坐標原點的對稱點,平行于![]() 的直線
的直線![]() 交
交![]() 于異于
于異于![]() 的兩點
的兩點![]() .點
.點![]() 關于原點的對稱點為
關于原點的對稱點為![]() .證明:直線
.證明:直線![]() 與
與![]() 軸圍成的三角形是等腰三角形.
軸圍成的三角形是等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 有兩個不同的零點
有兩個不同的零點![]() .
.
(ⅰ)求實數![]() 的取值范圍;
的取值范圍;
(ⅱ)求證:![]() .(其中
.(其中![]() 為
為![]() 的極小值點)
的極小值點)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】總體由編號為01,02,...,39,40的40個個體組成.利用下面的隨機數表選取5個個體,選取方法是從隨機數表(如下表)第1行的第4列和第5列數字開始由左到右依次選取兩個數字,則選出來的第5個個體的編號為( )
60 44 66 44 21
66 06 58 05 62
61 65 54 35 02
42 35 48 96 32
14 52 41 52 48
92 66 22 15 86
96 63 75 41 99
58 42 36 72 24
A.23B.21C.35D.32
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com