
【題目】近年來(lái)空氣質(zhì)量逐步惡化,霧霾天氣現(xiàn)象增多,大氣污染危害加重,大氣污染可引起心悸、呼吸困難等心肺疾病.為了解心肺疾病是否與性別有關(guān),在市第一人民醫(yī)院隨機(jī)對(duì)入院50人進(jìn)行了問(wèn)卷調(diào)查,得到如下的列聯(lián)表:
患心肺疾病 | 不患心肺疾病 | 合計(jì) | |||||||||
男 | 20 | 5 | 25 | ||||||||
女 | 10 | 15 | 25 | ||||||||
合計(jì) | 30 | 20 | 50 | ||||||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | ||||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | ||||
(1)是否有99.5%的把握認(rèn)為患心肺疾病與性別有關(guān)?說(shuō)明你的理由;(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,現(xiàn)在從患心肺疾病的10位女性中,選出3位進(jìn)行其他方面的排查,其中患胃病的人數(shù)為![]() ,求
,求![]() 的分布列、數(shù)學(xué)期望.參考公式:
的分布列、數(shù)學(xué)期望.參考公式:![]() ,其中
,其中![]()
【答案】(1)有99.5%的把握認(rèn)為是否患心肺疾病是與性別有關(guān)系的;
(2)![]()
![]() ;
;
【解析】試題分析:(1)計(jì)算觀測(cè)值K2,與7.879比較大小即可得出結(jié)論;
(2)利用超幾何分布的概率公式計(jì)算分布列,從而得出數(shù)學(xué)期望.
(1)∵![]() ,即
,即![]()
∴![]() ,又
,又![]() ,
,
∴我們有99.5%的把握認(rèn)為是否患心肺疾病是與性別有關(guān)系的
(2)現(xiàn)在從患心肺疾病的10位女性中選出3位,其中患胃病的人數(shù)![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布列為
的分布列為
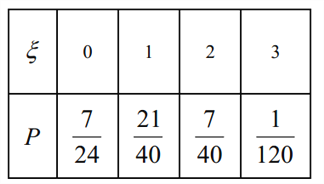
所以![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望
![]()
![]()


 新思維寒假作業(yè)系列答案
新思維寒假作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了解某班學(xué)生喜愛(ài)打籃球是否與性別有關(guān),對(duì)本班![]() 人進(jìn)行了問(wèn)卷調(diào)查得到了如下的列聯(lián)表:已知在全部
人進(jìn)行了問(wèn)卷調(diào)查得到了如下的列聯(lián)表:已知在全部![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人,抽到喜愛(ài)打籃球的學(xué)生的概率為
人,抽到喜愛(ài)打籃球的學(xué)生的概率為![]() .
.
(1)請(qǐng)將上面的列聯(lián)表補(bǔ)充完整(不用寫(xiě)計(jì)算過(guò)程);并求出:有多大把握認(rèn)為喜愛(ài)打籃球與性別有關(guān),說(shuō)明你的理由;
(2)若從該班不喜愛(ài)打籃球的男生中隨機(jī)抽取3人調(diào)查,求其中某男生甲被選到的概率。下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
(參考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】執(zhí)行如圖所示的程序框圖輸出的結(jié)果為( ) 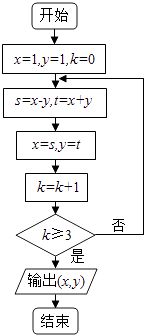
A.(﹣2,2)
B.(﹣4,0)
C.(﹣4,﹣4)
D.(0,﹣8)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知f(x)是定義在R上的偶函數(shù),f(x)在[0,+∞)上是增函數(shù),且f( ![]() )=0,則不等式f(
)=0,則不等式f( ![]() )>0的解集為( )
)>0的解集為( )
A.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
B.( ![]() ,1)∪(2,+∞)??
,1)∪(2,+∞)??
C.(0, ![]() )
)
D.(2,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】點(diǎn)M(x,y)與定點(diǎn)F(1,0)的距離和它到直線(xiàn)l:x=2的距離的比為 ![]() ,
,
(Ⅰ)求點(diǎn)M的軌跡.
(Ⅱ)是否存在點(diǎn)M到直線(xiàn) ![]() +y=1的距離最大?最大距離是多少?
+y=1的距離最大?最大距離是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】用數(shù)學(xué)歸納法證明“1+2+22+…+2n-1=2n-1(n∈N+)”的過(guò)程中,第二步n=k時(shí)等式成立,則當(dāng)n=k+1時(shí),應(yīng)得到( )
A.1+2+22+…+2k-2+2k-1=2k+1-1
B.1+2+22+…+2k+2k+1=2k-1+2k+1
C.1+2+22+…+2k-1+2k+1=2k+1-1
D.1+2+22+…+2k-1+2k=2k+1-1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓方程![]() 為:
為: ![]() ,
, ![]() 橢圓的右焦點(diǎn)為
橢圓的右焦點(diǎn)為![]() ,離心率為
,離心率為![]() ,直線(xiàn)
,直線(xiàn)![]() :
: ![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),且
兩點(diǎn),且![]()
(1)橢圓的方程及求![]() 的面積;
的面積;
(2)在橢圓上是否存在一點(diǎn)![]() ,使
,使![]() 為平行四邊形,若存在,求出
為平行四邊形,若存在,求出![]() 的取值范圍,若不存在說(shuō)明理由.
的取值范圍,若不存在說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)f(x)=ax2+bx+3在x=2時(shí)取得最小值,且函數(shù)f(x)的圖象在x軸上截得的線(xiàn)段長(zhǎng)為2.
(1)求函數(shù)f(x)的解析式;
(2)若函數(shù)g(x)=f(x)﹣mx的一個(gè)零點(diǎn)在區(qū)間(0,2)上,另一個(gè)零點(diǎn)在區(qū)間(2,3)上,求實(shí)數(shù)m的取值范圍.
(3)當(dāng)x∈[t,t+1]時(shí),函數(shù)f(x)的最小值為﹣ ![]() ,求實(shí)數(shù)t的值.
,求實(shí)數(shù)t的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com