
【題目】已知函數![]() .
.
(1)當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(2)若![]() 有兩個不同零點
有兩個不同零點![]() ,
,![]() ,證明:
,證明:![]() 且
且![]() .
.
【答案】(1)分類討論,詳見解析;(2)詳見解析.
【解析】
(1)求導后,令![]() 得
得![]() 或
或![]() ,按照
,按照![]() 與
與![]() 的大小分三種情況討論即可得到答案;
的大小分三種情況討論即可得到答案;
(2)根據(1)知![]() 時,函數的極小值大于0,因此函數
時,函數的極小值大于0,因此函數![]() 不可能有2個零點,故
不可能有2個零點,故![]() ,
,
所以![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,所以極小值
單調遞增,所以極小值![]() ,可得
,可得![]() ,再構造函數
,再構造函數![]() ,利用導數得到
,利用導數得到![]() 在
在![]() 上遞增,從而可得
上遞增,從而可得![]() 時,
時,![]() ,設
,設![]() ,則
,則![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 。
。
(1)![]() .
.
因為![]() ,由
,由![]() 得,
得,![]() 或
或![]() .
.
i)![]() 即
即![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,在
單調遞增,在![]() 單調遞減;
單調遞減;
ii)![]() 即
即![]() 時,
時,![]() 在
在![]() 單調遞減;
單調遞減;
iii)![]() 即
即![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.
單調遞減.
(2)由(1)知,![]() 時,
時,![]() 的極小值為
的極小值為![]() ,
,
![]() 時,
時,![]() 的極小值為
的極小值為![]() ,
,
![]() 時,
時,![]() 在
在![]() 單調,
單調,
故![]() 時,
時,![]() 至多有一個零點.
至多有一個零點.
當![]() 時,易知
時,易知![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
要使![]() 有兩個零點,則
有兩個零點,則![]() ,即
,即![]() ,得
,得![]() .
.
令![]() ,(
,(![]() ),則
),則![]()
![]()
![]()
![]() ,所以
,所以![]() 在
在![]() 時單調遞增,
時單調遞增,![]() ,
,![]() .
.
不妨設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
, ![]() .
.
由![]() 在
在![]() 單調遞減得,
單調遞減得,![]() ,即
,即![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】學校準備將![]() 名同學全部分配到運動會的田徑、拔河和球類
名同學全部分配到運動會的田徑、拔河和球類![]() 個不同項目比賽做志愿者,每個項目至少
個不同項目比賽做志愿者,每個項目至少![]() 名,則不同的分配方案有________種(用數字作答).
名,則不同的分配方案有________種(用數字作答).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點![]() 處下上至
處下上至![]() 處有兩種路徑.一種是從
處有兩種路徑.一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 沿索道乘纜車到
沿索道乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現有甲、乙兩位游客從
.現有甲、乙兩位游客從![]() 處下山,甲沿
處下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() .在甲出發
.在甲出發![]() 后,乙從
后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 后,再從
后,再從![]() 勻速步行到
勻速步行到![]() ,假設纜車勻速直線運動的速度為
,假設纜車勻速直線運動的速度為![]() ,山路
,山路![]() 長為1260
長為1260![]() ,經測量
,經測量![]() ,
,![]() .
.
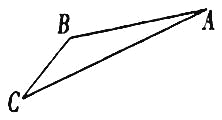
(1)求索道![]() 的長;
的長;
(2)問:乙出發多少![]() 后,乙在纜車上與甲的距離最短?
后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() ,乙步行的速度應控制在什么范圍內?
,乙步行的速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題
①命題“若![]() ,則
,則![]() ”的逆命題是真命題;
”的逆命題是真命題;
②若![]() ,
,![]() ,則
,則![]() 在
在![]() 上的投影是
上的投影是![]() ;
;
③在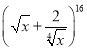 的二項展開式中,有理項共有4項;
的二項展開式中,有理項共有4項;
④已知一組正數![]() ,
,![]() ,
,![]() ,
,![]() 的方差為
的方差為![]() ,則數據
,則數據![]() ,
,![]() ,
,![]() ,
,![]() 的平均數為4;
的平均數為4;
⑤復數![]() 的共軛復數是
的共軛復數是![]() ,則
,則![]() .
.
其中真命題的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() ,定義
,定義![]() 為數列
為數列![]() 的一階差分數列,其中
的一階差分數列,其中![]() .
.
(1)若![]() ,試判斷
,試判斷![]() 是否是等差數列,并說明理由;
是否是等差數列,并說明理由;
(2)若![]() ,
,![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)對(2)中的數列![]() ,是否存在等差數列
,是否存在等差數列![]() ,使得
,使得![]() 對一切
對一切![]() 都成立,若存在,求出數列
都成立,若存在,求出數列![]() 的通項公式;若不存在,請說明理由.
的通項公式;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ;
;
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若![]() ,且
,且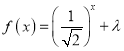 在閉區間
在閉區間![]() 上有實數解,求實數
上有實數解,求實數![]() 的范圍;
的范圍;
(3)如果函數![]() 的圖象過點
的圖象過點![]() ,且不等式
,且不等式![]() 對任意
對任意![]() 均成立,求實數
均成立,求實數![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sinx-xcosx-x,f′(x)為f(x)的導數.
(1)證明:f′(x)在區間(0,π)存在唯一零點;
(2)若x∈[0,π]時,f(x)≥ax,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直二面角α﹣l﹣β中,A∈α,B∈β,A,B都不在l上,AB與α所成角為x,AB與β所成角為y,AB與l所成角為z,則cos2x+cos2y+sin2z的值為( )
A.![]() B.2C.3D.
B.2C.3D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經市場調查,某商品每噸的價格為![]() 萬元時,該商品的月供給量為
萬元時,該商品的月供給量為![]() 噸,
噸,![]() ;月需求量為
;月需求量為![]() 噸,
噸,![]() ,當該商品的需求量大于供給量時,銷售量等于供給量;當該商品的需求量不大于供給量時,銷售量等于需求量,該商品的月銷售額等于月銷售量與價格的乘積.
,當該商品的需求量大于供給量時,銷售量等于供給量;當該商品的需求量不大于供給量時,銷售量等于需求量,該商品的月銷售額等于月銷售量與價格的乘積.
(1)已知![]() ,若某月該商品的價格為x=7,求商品在該月的銷售額(精確到1元);
,若某月該商品的價格為x=7,求商品在該月的銷售額(精確到1元);
(2)記需求量與供給量相等時的價格為均衡價格,若該商品的均衡價格不低于每噸6萬元,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com