
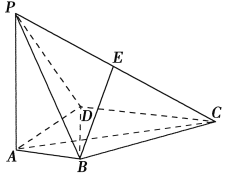
【題目】如圖,在四棱錐![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.
(1)(理科生做)證明:![]() ;
;
(文科生做)證明:![]() ;
;
(2)(理科生做)若![]() 為棱
為棱![]() 上一點,滿足
上一點,滿足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(文科生做)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析(2)理![]() ,文
,文![]()
【解析】
(1理)可通過以點![]() 為原點建立空間直角坐標系,然后確定
為原點建立空間直角坐標系,然后確定![]() 四點的坐標,最后通過求
四點的坐標,最后通過求![]() 得出
得出![]() ;
;
(1文)首先可證明四邊形![]() 是平行四邊形,再通過
是平行四邊形,再通過![]() 證明
證明![]() 平面
平面![]() ;
;
(2理)先求出向量![]() ,然后求出平面
,然后求出平面![]() 和平面
和平面![]() 的法向量,最后求出二面角
的法向量,最后求出二面角![]() 的余弦值;
的余弦值;
(2文)可通過等面積法求出點![]() 到平面
到平面![]() 的距離。
的距離。
(1理)依題意,以點![]() 為原點建立空間直角坐標系(如圖),
為原點建立空間直角坐標系(如圖),
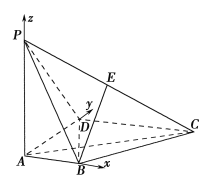 可得
可得![]() ,
,
![]() ,
,
由![]() 為棱
為棱![]() 的中點,
的中點,
得![]() ,
,
向量![]() ,
,![]() ,故
,故![]() ,
,
所以![]() .
.
(1文)取![]() 中點
中點![]() ,聯接
,聯接![]()
因為![]() 是
是![]() 中點,所以
中點,所以![]() 且
且![]()
所以![]() 且
且![]() ,四邊形
,四邊形![]() 是平行四邊形
是平行四邊形
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2理)向量![]() ,
,![]() ,
,![]() ,
,![]() .
.
由點![]() 在棱
在棱![]() 上,設
上,設![]() ,
,
故![]()
由![]() ,得
,得![]() ,因此
,因此![]() ,解得
,解得![]() ,
,
即![]() ,設
,設![]() 為平面
為平面![]() 的法向量,
的法向量,
則 ,即
,即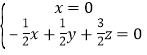 ,
,
不妨令![]() ,可得
,可得![]() 平面
平面![]() 的一個法向量.
的一個法向量.
取平面![]() 的法向量
的法向量![]() ,則
,則
![]() ,
,
易知,二面角![]() 是銳角,所以其余弦值為
是銳角,所以其余弦值為![]()
(2文)設![]() 到平面
到平面![]() 距離為
距離為![]() ,
,
![]()
在![]() 中,
中,![]() 因為
因為![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
所以![]() ,在
,在![]() 中,
中,![]()
將數據代入得![]() 。
。


科目:高中數學 來源: 題型:
【題目】用6種顏色給右圖四面體A﹣BCD的每條棱染色,要求每條棱只染一種顏色且共頂點的棱染不同的顏色,則不同的染色方法共有( )種. 
A.4080
B.3360
C.1920
D.720
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,點
,點![]() 為棱
為棱![]() 的中點,點
的中點,點![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 與
與![]() 交于點
交于點![]() ,則異面直線
,則異面直線![]() 與
與![]() 所成角的正切值為__________.
所成角的正切值為__________.
【答案】![]()
【解析】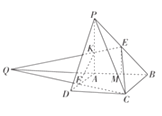
延長![]() 交
交![]() 的延長線與點Q,連接QE交PA于點K,設QA=x,
的延長線與點Q,連接QE交PA于點K,設QA=x,
由![]() ,得
,得![]() ,則
,則![]() ,所以
,所以![]() .
.
取![]() 的中點為M,連接EM,則
的中點為M,連接EM,則![]() ,
,
所以![]() ,則
,則![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得異面直線![]() 與
與![]() 所成角即為
所成角即為![]() ,
,
則異面直線![]() 與
與![]() 所成角的正切值為
所成角的正切值為![]() .
.
【題型】填空題
【結束】
17
【題目】在極坐標系中,極點為![]() ,已知曲線
,已知曲線![]() :
: ![]() 與曲線
與曲線![]() :
: ![]() 交于不同的兩點
交于不同的兩點![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求過點![]() 且與直線
且與直線![]() 平行的直線
平行的直線![]() 的極坐標方程.
的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,點
,點![]() 滿足
滿足![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)若直線![]() 過點
過點![]() 且與軌跡
且與軌跡![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(i)無論直線![]() 繞點
繞點![]() 怎樣轉動,在
怎樣轉動,在![]() 軸上總存在定點
軸上總存在定點![]() ,使
,使![]() 恒成立,求實數
恒成立,求實數![]() 的值.
的值.
(ii)在(i)的條件下,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①命題:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 則x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,則x0∈(0,+∞),f(x0)=1;
,則x0∈(0,+∞),f(x0)=1;
④等差數列{an}的前n項和為Sn , 若a4=3,則S7=21;
⑤在△ABC中,若A>B,則sinA>sinB.
其中真命題是 . (只填寫序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
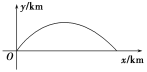
【題目】如圖,建立平面直角坐標系,x軸在地平面上,y軸垂直于地平面,單位長度為1 km,某炮位于原點.已知炮彈發射后的軌跡在方程y=kx-![]() (1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.則炮的最大射程為( )
(1+k2)x2(k>0)表示的曲線上,其中k與發射方向有關.炮的射程是指炮彈落地點的橫坐標.則炮的最大射程為( )
A. 20 km B. 10 km
C. 5 km D. 15 km
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一次函數f(x)=ax-2.
(1)當a=3時,解不等式|f(x)|<4;
(2)解關于x的不等式|f(x)|<4;
(3)若關于x的不等式|f(x)|≤3對任意x∈[0,1]恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com