【題目】已知下列命題：
①命題：x∈（0，2），3x＞x3的否定是：x∈（0，2），3x≤x3；
②若f（x）=2x﹣2﹣x ， 則x∈R，f（﹣x）=﹣f（x）；
③若f（x）=x+ 
，則x0∈（0，+∞），f（x0）=1；
④等差數列{an}的前n項和為Sn ， 若a4=3，則S7=21；
⑤在△ABC中，若A＞B，則sinA＞sinB．
其中真命題是 ． （只填寫序號）
【答案】①②④⑤
【解析】解：對于①，命題：x∈（0，2），3x＞x3的否定是：x∈（0，2），3x≤x3 ， 正確；
對于②，若f（x）=2x﹣2﹣x ， 則x∈R，f（﹣x）=﹣f（x），正確；
對于③，對于函數f（x）=x+ 
，當且僅當x=0時，f（x）=1，故錯；
對于④，等差數列{an}的前n項和為Sn ， 若a4=3， 
，故正確；
對于⑤，在△ABC中，若A＞B，則a＞b2RsinA＞2RsinBsinA＞sinB，故正確．
所以答案是：①②④⑤
【考點精析】掌握命題的真假判斷與應用是解答本題的根本，需要知道兩個命題互為逆否命題，它們有相同的真假性；兩個命題為互逆命題或互否命題，它們的真假性沒有關系．
科目：高中數學 來源： 題型：
【題目】已知正項數列{an}的前n項和為Sn ， 且 
是1與an的等差中項．
（1）求數列{an}的通項公式；
（2）設Tn為數列{ 
}的前n項和，證明： 
≤Tn＜1（n∈N*）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】先把函數y=sin（x+φ）的圖象上個點的橫坐標縮短為原來的 
（縱坐標不變），再向右平移 
個單位，所得函數關于y軸對稱，則φ的值可以是（ ）
A.
B.
C.-
D.-
查看答案和解析>>
科目：高中數學 來源： 題型：
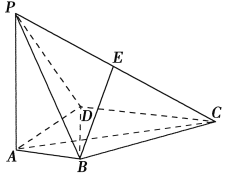
【題目】如圖，在四棱錐
中，
⊥底面
，
，
，
，
，點
為棱
的中點．
(1)（理科生做）證明：
；
（文科生做）證明：
；
(2)（理科生做）若
為棱上一點，滿足
，求二面角
的余弦值．
（文科生做）求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數學家歐拉在1765年發現，任意三角形的外心、重心、垂心位于同一條直線上，這條直線稱為歐拉線已知
的頂點
，若其歐拉線的方程為
，則頂點
的坐標為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（a>b>0）的上、下、左、右四個頂點分別為A，B，C，D，x軸正半軸上的點P滿足|PA|=|PD|=2，|PC|=4。
（I）求橢圓C的標準方程以及點P的坐標；
（II）過點P作直線l交橢圓C于點M，N，是否存在這樣的直線l使得△MNA和△MND的面積相等？若存在，請求出直線l的方程，若不存在，請說明理由；
（III）在（II）的條件下，求當直線l的傾斜角為鈍角時△MND的面積。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(本小題滿分12分)
已知關于
的不等式
，其中
.
（1）當
變化時，試求不等式的解集
；
（2）對于不等式的解集，若滿足
（其中
為整數集）. 試探究集合
能否為有限集？若 能，求出使得集合中元素個數最少的的所有取值，并用列舉法表示集合；若不能，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐C﹣PAB中，AB⊥BC，PB⊥BC，PA=PB=5，AB=6，BC=4，點M是PC的中點，點N在線段AB上，且MN⊥AB． 
（1）求AN的長；
（2）求銳二面角P﹣NC﹣A的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
