
【題目】隨著手機的發展,“微信”逐漸成為人們支付購物的一種形式.某機構對“使用微信支付”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信支付”贊成人數如下表.
年齡 (單位:歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡45歲為分界點”,由以上計數據完成下面![]() 列聯表,并判斷是否有99%的把握認為“使用微信支付”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信支付”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在![]() 的被調查人中按照贊成與不贊成分層抽樣,抽取5人進行追蹤調查,在5人中抽取3人做專訪,求3人中不贊成使用微信支付的人數的分布列和期望值.
的被調查人中按照贊成與不贊成分層抽樣,抽取5人進行追蹤調查,在5人中抽取3人做專訪,求3人中不贊成使用微信支付的人數的分布列和期望值.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
科目:高中數學 來源: 題型:
【題目】現給出三個條件:①函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;②函數
對稱;②函數![]() 的圖象關于點
的圖象關于點![]() 對稱;③函數
對稱;③函數![]() 的圖象上相鄰兩個最高點的距離為
的圖象上相鄰兩個最高點的距離為![]() .從中選出兩個條件補充在下面的問題中,并以此為依據求解問題.
.從中選出兩個條件補充在下面的問題中,并以此為依據求解問題.
已知函數![]() (
(![]() ,
,![]() ),_____,_____.求函數
),_____,_____.求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,平面ABCD⊥平面PAD,AD∥BC,AB=BC![]() AD=1,∠APD=∠BAD=90°.
AD=1,∠APD=∠BAD=90°.
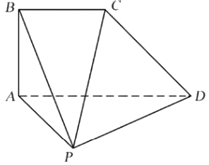
(1)求證:PD⊥PB;
(2)當PA=PD時,求三棱錐P﹣BCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中,曲線C的參數方程為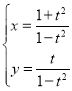 (t為參數).以原點O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρcos(
(t為參數).以原點O為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρcos(![]() )
)![]() .
.
(1)求曲線C和直線l的直角坐標方程;
(2)若直線l交曲線C于A,B兩點,交x軸于點P,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上位于
上位于![]() 軸兩側的不同兩點
軸兩側的不同兩點
(1)若![]() 在直線
在直線![]() 上,且使得以
上,且使得以![]() 為頂點的四邊形恰為正方形,求該正方形的面積.
為頂點的四邊形恰為正方形,求該正方形的面積.
(2)求過![]() 、
、![]() 的切線與直線
的切線與直線![]() 圍成的三角形面積的最小值;
圍成的三角形面積的最小值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某濕地公園的鳥瞰圖是一個直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 長1千米,
長1千米,![]() 長
長![]() 千米,公園內有一個形狀是扇形的天然湖泊
千米,公園內有一個形狀是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 長為半徑,弧
長為半徑,弧![]() 為湖岸,其余部分為灘地,B,D點是公園的進出口.公園管理方計劃在進出口之間建造一條觀光步行道:線段
為湖岸,其余部分為灘地,B,D點是公園的進出口.公園管理方計劃在進出口之間建造一條觀光步行道:線段![]() 線段
線段![]() 弧
弧![]() ,其中Q在線段
,其中Q在線段![]() 上(異于線段端點),
上(異于線段端點),![]() 與弧
與弧![]() 相切于P點(異于弧端點]根據市場行情
相切于P點(異于弧端點]根據市場行情![]() ,
,![]() 段的建造費用是每千米10萬元,湖岸段弧
段的建造費用是每千米10萬元,湖岸段弧![]() 的建造費用是每千米
的建造費用是每千米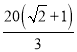 萬元(步行道的寬度不計),設
萬元(步行道的寬度不計),設![]() 為
為![]() 弧度觀光步行道的建造費用為
弧度觀光步行道的建造費用為![]() 萬元.
萬元.
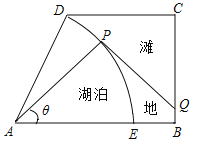
(1)求步行道的建造費用![]() 關于
關于![]() 的函數關系式,并求其走義域;
的函數關系式,并求其走義域;
(2)當![]() 為何值時,步行道的建造費用最低?
為何值時,步行道的建造費用最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com