
【題目】如圖,在四棱錐P﹣ABCD中,平面ABCD⊥平面PAD,AD∥BC,AB=BC![]() AD=1,∠APD=∠BAD=90°.
AD=1,∠APD=∠BAD=90°.
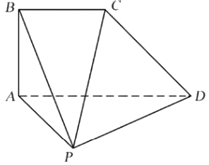
(1)求證:PD⊥PB;
(2)當PA=PD時,求三棱錐P﹣BCD的體積.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)推導出BA⊥AD,BA⊥PD,AP⊥PD,從而PD⊥平面PAB,由此能證明PD⊥PB;
(2)取AD中點O,連接PO,則PO⊥AD,證明PO⊥平面ABCD,再由棱錐體積公式求解.
(1)∵∠BAD=90°,∴BA⊥AD,
∵平面ABCD⊥平面PAD,交線為AD,
∴BA⊥平面PAD,從而BA⊥PD,
∵∠APD=90°,∴AP⊥PD,
∵BA∩AP=A,∴PD⊥平面PAB,
∵PB平面PAB,∴PD⊥PB;
(2)∵PA=PD,取AD中點O,連接PO,則PO⊥AD,

由平面ABCD⊥平面PAD,交線為AD,得PO⊥平面ABCD.
又∠APD=90°,AD=2,得PO=1,
∴![]() .
.
即三棱錐P﹣BCD的體積為![]() .
.


科目:高中數學 來源: 題型:
【題目】環境問題是當今世界共同關注的問題,我國環保總局根據空氣污染指數![]() 濃度,制定了空氣質量標準:
濃度,制定了空氣質量標準:
空氣污染質量 |
|
|
|
|
|
|
空氣質量等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
某市政府為了打造美麗城市,節能減排,從2010年開始考查了連續六年11月份的空氣污染指數,繪制了頻率分布直方圖,經過分析研究,決定從2016年11月1日起在空氣質量重度污染和嚴重污染的日子對機動車輛限號出行,即車牌尾號為單號的車輛單號出行,車牌尾號為雙號的車輛雙號出行(尾號為字母的,前13個視為單號,后13個視為雙號).
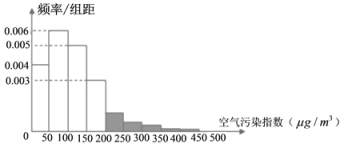
(1)某人計劃11月份開車出行,求因空氣污染被限號出行的概率;
(2)該市環保局為了調查汽車尾氣排放對空氣質量的影響,對限行三年來的11月份共90天的空氣質量進行統計,其結果如表:
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
天數 | 16 | 39 | 18 | 10 | 5 | 2 |
根據限行前六年180天與限行后90天的數據,計算并填寫![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為空氣質量的優良與汽車尾氣的排放有關.
的把握認為空氣質量的優良與汽車尾氣的排放有關.
空氣質量優良 | 空氣質量污染 | 合計 | |
限行前 | |||
限行后 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 其中
其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國全面二孩政策已于2016年1月1日起正式實施.國家統計局發布的數據顯示,從2012年到2017年,中國的人口自然增長率變化始終不大,在5‰上下波動(如圖).

為了了解年齡介于24歲至50歲之間的適孕夫妻對生育二孩的態度如何,統計部門按年齡分為9組,每組選取150對夫妻進行調查統計有生育二孩意愿的夫妻數,得到下表:
年齡區間 |
|
|
|
|
|
|
|
|
|
有意愿數 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)設每個年齡區間的中間值為![]() ,有意愿數為
,有意愿數為![]() ,求樣本數據的線性回歸直線方程,并求該模型的相關系數
,求樣本數據的線性回歸直線方程,并求該模型的相關系數![]() (結果保留兩位小數);
(結果保留兩位小數);
(2)從![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 這五個年齡段中各選出一對夫妻(能代表該年齡段超過半數夫妻的意愿)進一步調研,再從這5對夫妻中任選2對夫妻.求其中恰有一對不愿意生育二孩的夫妻的概率.
這五個年齡段中各選出一對夫妻(能代表該年齡段超過半數夫妻的意愿)進一步調研,再從這5對夫妻中任選2對夫妻.求其中恰有一對不愿意生育二孩的夫妻的概率.
(參考數據和公式: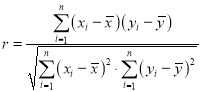 ,
,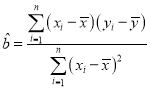 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車品牌為了了解客戶對于其旗下的五種型號汽車的滿意情況,隨機抽取了一些客戶進行回訪,調查結果如下表:
汽車型號 | I | II | III | IV | V |
回訪客戶(人數) | 250 | 100 | 200 | 700 | 350 |
滿意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
滿意率是指:某種型號汽車的回訪客戶中,滿意人數與總人數的比值.
假設客戶是否滿意互相獨立,且每種型號汽車客戶對于此型號汽車滿意的概率與表格中該型號汽車的滿意率相等.
(1)從所有的回訪客戶中隨機抽取1人,求這個客戶滿意的概率;
(2)從I型號和V型號汽車的所有客戶中各隨機抽取1人,設其中滿意的人數為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分別表示I, II, III, IV, V型號汽車讓客戶滿意, “
”分別表示I, II, III, IV, V型號汽車讓客戶滿意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分別表示I, II, III, IV, V型號汽車讓客戶不滿意.寫出方差
” 分別表示I, II, III, IV, V型號汽車讓客戶不滿意.寫出方差![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中華人民共和國的國旗是五星紅旗,旗面左上方綴著五顆黃色五角星,四顆小星環拱在一顆大星之后,并各有一個角尖正對大星的中心點,象征著中國共產黨領導下的革命人民大團結和中國人民對黨的衷心擁護.五角星可以通過正五邊形連接對角線得到,如圖所示,在正五邊形ABCDE內部任取一點,則該點取自陰影部分的概率為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的中a1=1,a2=2,且滿足![]() .
.
(1)求數列{an}的通項公式;
(2)設bn![]() ,記數列{bn}的前n項和為Tn,若|Tn+1|
,記數列{bn}的前n項和為Tn,若|Tn+1|![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著手機的發展,“微信”逐漸成為人們支付購物的一種形式.某機構對“使用微信支付”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信支付”贊成人數如下表.
年齡 (單位:歲) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡45歲為分界點”,由以上計數據完成下面![]() 列聯表,并判斷是否有99%的把握認為“使用微信支付”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信支付”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在![]() 的被調查人中按照贊成與不贊成分層抽樣,抽取5人進行追蹤調查,在5人中抽取3人做專訪,求3人中不贊成使用微信支付的人數的分布列和期望值.
的被調查人中按照贊成與不贊成分層抽樣,抽取5人進行追蹤調查,在5人中抽取3人做專訪,求3人中不贊成使用微信支付的人數的分布列和期望值.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,且保費與上一年度車輛發生道路交通事故的情況相聯系.發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:
元,在下一年續保時,實行的是費率浮動機制,且保費與上一年度車輛發生道路交通事故的情況相聯系.發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:
交強險浮動因素和費率浮動比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮 |
| 上兩個年度未發生有責任道路交通事故 | 下浮 |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮 |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 |
|
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮 |
| 上一個年度發生有責任道路交通死亡事故 | 上浮 |
某機構為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了60輛車齡已滿三年該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一輛普通6座以下私家車在第四年續保時保費高于基本保費的頻率;
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車.假設購進一輛事故車虧損5000元,一輛非事故車盈利10000元.且各種投保類型車的頻率與上述機構調查的頻率一致,完成下列問題:
①若該銷售商店內有6輛(車齡已滿三年)該品牌二手車,某顧客欲在店內隨機挑選2輛車,求這2輛車恰好有一輛為事故車的概率;
②若該銷售商一次購進120輛(車齡已滿三年)該品牌二手車,求一輛車盈利的平均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com