【題目】已知函數
ae2x+(a﹣2) ex﹣x.
（1）討論
的單調性；
（2）若
有兩個零點，求a的取值范圍.
【答案】（1）見解析；（2）
.
【解析】試題分析：（1）討論
單調性，首先進行求導，發現式子特點后要及時進行因式分解，再對
按
， 
進行討論，寫出單調區間；（2）根據第（1）問，若
， 
至多有一個零點.若
，當
時， 
取得最小值，求出最小值
，根據
， 
， 
進行討論，可知當
時有2個零點.易知
在
有一個零點；設正整數
滿足
，則
.由于
，因此
在
有一個零點.從而可得
的取值范圍為
.
試題解析：（1）
的定義域為
， 
，
（ⅰ）若
，則
，所以
在
單調遞減.
（ⅱ）若
，則由
得
.
當
時， 
；當
時， 
，所以
在
單調遞減，在
單調遞增.
（2）（ⅰ）若
，由（1）知， 
至多有一個零點.
（ⅱ）若
，由（1）知，當
時， 
取得最小值，最小值為
.
①當
時，由于
，故
只有一個零點；
②當
時，由于
，即
，故
沒有零點；
③當
時， 
，即
.
又
，故
在
有一個零點.
設正整數
滿足
，則
.
由于
，因此
在
有一個零點.
綜上， 
的取值范圍為
.
點睛:研究函數零點問題常常與研究對應方程的實根問題相互轉化.已知函數
有2個零點求參數a的取值范圍，第一種方法是分離參數，構造不含參數的函數，研究其單調性、極值、最值，判斷
與其交點的個數，從而求出a的取值范圍；第二種方法是直接對含參函數進行研究，研究其單調性、極值、最值，注意點是若
有2個零點，且函數先減后增，則只需其最小值小于0，且后面還需驗證最小值兩邊存在大于0的點.
科目：高中數學 來源： 題型：
【題目】在2018年俄羅斯世界杯期間,莫斯科的部分餐廳經營了來自中國的小龍蝦,這些小龍蝦標有等級代碼.為得到小龍蝦等級代碼數值
與銷售單價
之間的關系,經統計得到如下數據：
等級代碼數值 | 38 | 48 | 58 | 68 | 78 | 88 |
銷售單價 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知銷售單價與等級代碼數值之間存在線性相關關系,求關于的線性回歸方程(系數精確到0.1)；
（2）若莫斯科某個餐廳打算從上表的6種等級的中國小龍蝦中隨機選2種進行促銷，記被選中的2種等級代碼數值在60以下（不含60）的數量為
，求的分布列及數學期望.
參考公式：對一組數據
,
，
,其回歸直線
的斜率和截距最小二乘估計分別為：
,
.
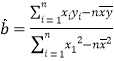參考數據：
,
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心在直線
上的圓C經過
點，且與直線
相切.
（1）求過點P且被圓C截得的弦長等于4的直線方程；
（2）過點P作兩條相異的直線分別與圓C交于A，B，若直線PA，PB的傾斜角互補，試判斷直線AB與OP的位置關系（O為坐標原點），并證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，已知圓心
在直線
上的圓
經過點
，但不經過坐標原點，并且直線
與圓
相交所得的弦長為4.
（1）求圓
的一般方程；
（2）若從點
發出的光線經過
軸反射，反射光線剛好通過圓
的圓心，求反射光線所在的直線方程（用一般式表達）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中正確的個數是（ ）
①由五個面圍成的多面體只能是三棱柱；
②由若干個平面多邊形所圍成的幾何體是多面體；
③僅有一組對面平行的五面體是棱臺；
④有一面是多邊形，其余各面是三角形的幾何體是棱錐.
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，三國時代數學家趙爽在《周髀算經》中利用弦圖，給出了勾股定理的絕妙證明.圖中包含四個全等的直角三角形及一個小正方形（陰影），設直角三角形有一內角為
，若向弦圖內隨機拋擲500顆米粒（大小忽略不計，取
），則落在小正方形（陰影）內的米粒數大約為（ ）
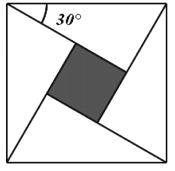
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了對某課題進行研究，分別從A，B，C三所高校中用分層隨機抽樣法抽取若干名教授組成研究小組，其中高校A有m名教授，高校B有72名教授，高校C有n名教授（其中
）
（1）若A，B兩所高校中共抽取3名教授，B，C兩所高校中共抽取5名教授，求m，n；
（2）若高校B中抽取的教授數是高校A和C中抽取的教授總數的
，求三所高校的教授的總人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
