
【題目】在直角坐標系![]() 中,過點
中,過點![]() 作直線
作直線![]() 交
交![]() 軸于A點、交
軸于A點、交![]() 軸于B點,且P位于AB兩點之間.
軸于B點,且P位于AB兩點之間.
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)求當![]() 取得最小值時直線
取得最小值時直線![]() 的方程;
的方程;
(3)當![]() 面積最小值時的直線方程.
面積最小值時的直線方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
設直線![]() 可求出
可求出![]() ,
,![]() .結合
.結合![]() 位于
位于![]() 之間,建立關于
之間,建立關于![]() 的不等式,可得
的不等式,可得![]() .
.
(1)由![]() 的坐標,得出向量
的坐標,得出向量![]() 和
和![]() 坐標,從而將
坐標,從而將![]() 化為關于
化為關于![]() 的方程,解出
的方程,解出![]() 值,即得直線
值,即得直線![]() 的方程;
的方程;
(2)由向量數量積的坐標運算公式,得出![]() 關于
關于![]() 的表達式,再用基本不等式得到
的表達式,再用基本不等式得到![]() 取得最小值時
取得最小值時![]() 的斜率
的斜率![]() ,從而得到直線
,從而得到直線![]() 的方程.
的方程.
(3)求出![]() ,再利用基本不等式求最小值,從而得到等號成立的條件,即
,再利用基本不等式求最小值,從而得到等號成立的條件,即![]() ,由此能求出當
,由此能求出當![]() 面積最小值時的直線方程.
面積最小值時的直線方程.
由題意知,直線![]() 的斜率
的斜率![]() 存在且
存在且![]() ,
,
設![]() ,得令
,得令![]() ,得
,得![]() ,所以
,所以![]() ,
,
再令![]() ,得
,得![]() ,所以
,所以![]() ,
,
∵點![]() 位于
位于![]() 兩點之間,∴
兩點之間,∴![]() 且
且![]() ,解得
,解得![]() .
.
∴![]() ,
,![]() ,
,
(1)∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴直線![]() 的方程為
的方程為![]() ,整理得
,整理得![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
當![]() ,即
,即![]() 時,等號成立.
時,等號成立.
∴當![]() 取得最小值時直線
取得最小值時直線![]() 的方程為
的方程為![]() ,
,
化為一般式:![]() .
.
(3)∵![]() ,
,![]() ,
,![]() ,
,
∴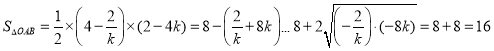 ,
,
當![]() 時,即
時,即![]() 時,取等號,
時,取等號,
∴當![]() 面積最小值時的直線方程為
面積最小值時的直線方程為![]() ,即
,即![]() .
.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
【題目】一個經銷鮮花產品的微店,為保障售出的百合花品質,每天從云南鮮花基地空運固定數量的百合花,如有剩余則免費分贈給第二天購花顧客,如果不足,則從本地鮮花供應商處進貨.今年四月前10天,微店百合花的售價為每支2元,云南空運來的百合花每支進價1.6元,本地供應商處百合花每支進價1.8元,微店這10天的訂單中百合花的需求量(單位:支)依次為:251,255,231,243,263,241,265,255,244,252.
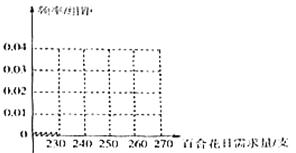
(Ⅰ)求今年四月前10天訂單中百合花需求量的平均數和眾數,并完成頻率分布直方圖;
(Ⅱ)預計四月的后20天,訂單中百合花需求量的頻率分布與四月前10天相同,百合花進貨價格與售價均不變,請根據(Ⅰ)中頻率分布直方圖判斷(同一組中的需求量數據用該組區間的中點值作代表,位于各區間的頻率代替位于該區間的概率),微店每天從云南固定空運250支,還是255支百合花,四月后20天百合花銷售總利潤會更大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,其中
,其中![]() ,
,![]() .如果集合
.如果集合![]() 滿足:對于任意的
滿足:對于任意的![]() ,都有
,都有![]() ,那么稱集合
,那么稱集合![]() 具有性質
具有性質![]() .
.
(Ⅰ)寫出一個具有性質![]() 的集合
的集合![]() ;
;
(Ⅱ)證明:對任意具有性質![]() 的集合
的集合![]() ,
,![]() ;
;
(Ⅲ)求具有性質![]() 的集合
的集合![]() 的個數.
的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查消費者的維權意識,青島二中的學生記者在五四廣場隨機調查了120名市民,按他們的年齡分組:第1組[20.30),第2組[30,40),第3組[40,50),第4組[50,60),第5組[60,70),得到的頻率分布直方圖如圖所示.
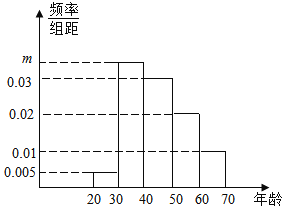
(1)若要從被調查的市民中選1人采訪,求被采訪人恰好在第2組或第5組的概率;
(2)已知第1組市民中男性有2人,學生要從第1組中隨機抽取3名市民組成維權志愿者服務隊,求至少有兩名女性的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 1(a>b>0)的右焦點為F,A(2,0)是橢圓的右頂點,過F且垂直于x軸的直線交橢圓于P,Q兩點,且|PQ|=3.
1(a>b>0)的右焦點為F,A(2,0)是橢圓的右頂點,過F且垂直于x軸的直線交橢圓于P,Q兩點,且|PQ|=3.
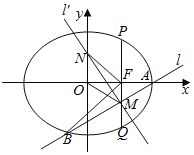
(1)求橢圓的方程;
(2)過點A的直線l與橢圓交于另一點B,垂直于l的直線l′與直線l交于點M,與y軸交于點N,若FB⊥FN且|MO|=|MA|,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() ,
,![]() 為
為![]() 中點現將四邊形
中點現將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如圖②所示的多面體在圖②中,
,得到如圖②所示的多面體在圖②中,
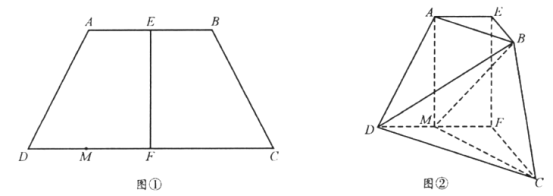
(1)證明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .將梯形
.將梯形![]() 沿直線
沿直線![]() 折起,使
折起,使![]() 平面
平面![]() ,如圖2,
,如圖2,![]() 分別是
分別是![]() 上的點.
上的點.
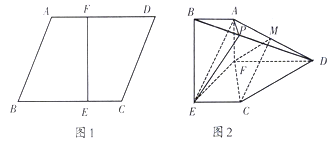
(1)求證:圖2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以坐標原點
),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)若![]() ,求直線
,求直線![]() 的普通方程及曲線
的普通方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 有兩個不同的交點,求
有兩個不同的交點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種植園在芒果臨近成熟時,隨機從一些芒果樹上摘下100個芒果,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經統計得頻率分布直方圖如圖所示.
(單位:克)中,經統計得頻率分布直方圖如圖所示.

(1) 經計算估計這組數據的中位數;
(2)現按分層抽樣從質量為![]() ,
,![]() 的芒果中隨機抽取
的芒果中隨機抽取![]() 個,再從這
個,再從這![]() 個中隨機抽取
個中隨機抽取![]() 個,求這
個,求這![]() 個芒果中恰有
個芒果中恰有![]() 個在
個在![]() 內的概率.
內的概率.
(3)某經銷商來收購芒果,以各組數據的中間數代表這組數據的平均值,用樣本估計總體,該種植園中還未摘下的芒果大約還有![]() 個,經銷商提出如下兩種收購方案:
個,經銷商提出如下兩種收購方案:
A:所以芒果以![]() 元/千克收購;
元/千克收購;
B:對質量低于![]() 克的芒果以
克的芒果以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.
元/個收購.
通過計算確定種植園選擇哪種方案獲利更多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com