
【題目】△ABC的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求C;
(2)若c= ![]() ,△ABC的面積為
,△ABC的面積為 ![]() ,求△ABC的周長(zhǎng).
,求△ABC的周長(zhǎng).
【答案】
(1)解:已知等式利用正弦定理化簡(jiǎn)得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
∵sinC≠0,sin(A+B)=sinC
∴cosC= ![]() ,
,
又0<C<π,
∴C= ![]() ;
;
(2)解:由余弦定理得7=a2+b2﹣2ab ![]() ,
,
∴(a+b)2﹣3ab=7,
∵S= ![]() absinC=
absinC= ![]() ab=
ab= ![]() ,
,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周長(zhǎng)為5+ ![]()
【解析】(1)已知等式利用正弦定理化簡(jiǎn),整理后利用兩角和與差的正弦函數(shù)公式及誘導(dǎo)公式化簡(jiǎn),根據(jù)sinC不為0求出cosC的值,即可確定出出C的度數(shù);(2)利用余弦定理列出關(guān)系式,利用三角形面積公式列出關(guān)系式,求出a+b的值,即可求△ABC的周長(zhǎng).


 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某園林基地培育了一種新觀賞植物,經(jīng)過一年的生長(zhǎng)發(fā)育,技術(shù)人員從中抽取了部分植株的高度(單位:厘米)作為樣本(樣本容量為![]() )進(jìn)行統(tǒng)計(jì),按照
)進(jìn)行統(tǒng)計(jì),按照![]()
![]() 的分組作出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在
的分組作出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在![]() 的數(shù)據(jù)).
的數(shù)據(jù)).
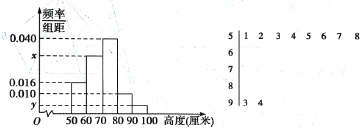
(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)在選取的樣本中,從高度在![]() 厘米以上(含
厘米以上(含![]() 厘米)的植株中隨機(jī)抽取
厘米)的植株中隨機(jī)抽取![]() 株,求所取的
株,求所取的![]() 株中至少有一株高度在
株中至少有一株高度在![]() 內(nèi)的概率.
內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓C:![]() +
+![]() =1(a>b>0)的短軸兩端點(diǎn)為B1(0,﹣1)、B2(0,1),離心率e=
=1(a>b>0)的短軸兩端點(diǎn)為B1(0,﹣1)、B2(0,1),離心率e=![]() ,點(diǎn)P是橢圓C上不在坐標(biāo)軸上的任意一點(diǎn),直線B1P和B2P分別與x軸相交于M,N兩點(diǎn),
,點(diǎn)P是橢圓C上不在坐標(biāo)軸上的任意一點(diǎn),直線B1P和B2P分別與x軸相交于M,N兩點(diǎn),

(1)求橢圓![]() 的方程和
的方程和![]() 的值;
的值;
(2)若點(diǎn)![]() 坐標(biāo)為(1,0),過
坐標(biāo)為(1,0),過![]() 點(diǎn)的直線
點(diǎn)的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點(diǎn),試求
兩點(diǎn),試求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下面有四個(gè)命題:
①函數(shù)y=tan x在每一個(gè)周期內(nèi)都是增函數(shù).
②函數(shù)y=sin(2x+ ![]() )的圖象關(guān)于直線x=
)的圖象關(guān)于直線x= ![]() 對(duì)稱;
對(duì)稱;
③函數(shù)y=tanx的對(duì)稱中心(kπ,0),k∈Z.
④函數(shù)y=sin(2x﹣ ![]() )是偶函數(shù).
)是偶函數(shù).
其中正確結(jié)論個(gè)數(shù)( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一只口袋中裝有形狀、大小都相同的10個(gè)小球,其中有紅球2個(gè),黑球3個(gè),白球5個(gè).
![]() 從中1次隨機(jī)摸出2個(gè)球,求2個(gè)球顏色相同的概率;
從中1次隨機(jī)摸出2個(gè)球,求2個(gè)球顏色相同的概率;
![]() 從中1次隨機(jī)摸出3個(gè)球,記白球的個(gè)數(shù)為X,求隨機(jī)變量X的概率分布和數(shù)學(xué)期望
從中1次隨機(jī)摸出3個(gè)球,記白球的個(gè)數(shù)為X,求隨機(jī)變量X的概率分布和數(shù)學(xué)期望![]() ;
;
![]() 每次從袋中隨機(jī)摸出1個(gè)球,記下顏色后放回,連續(xù)取3次,求取到紅球的次數(shù)大于取到白球的次數(shù)的概率.
每次從袋中隨機(jī)摸出1個(gè)球,記下顏色后放回,連續(xù)取3次,求取到紅球的次數(shù)大于取到白球的次數(shù)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=lnx+ ![]() ,m∈R
,m∈R
(1)當(dāng)m=e(e為自然對(duì)數(shù)的底數(shù))時(shí),求f(x)的最小值;
(2)討論函數(shù)g(x)=f′(x)﹣ ![]() 零點(diǎn)的個(gè)數(shù);
零點(diǎn)的個(gè)數(shù);
(3)(理科)若對(duì)任意b>a>0, ![]() <1恒成立,求m的取值范圍.
<1恒成立,求m的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com