
【題目】如圖①,△ABC是以AC為斜邊的等腰直角三角形,△BCD是等邊三角形.如圖②,將△BCD沿BC折起,使平面BCD⊥平面ABC,記BC的中點為E,BD的中點為M,點F、N在棱AC上,且AF=3CF,C![]() .
.
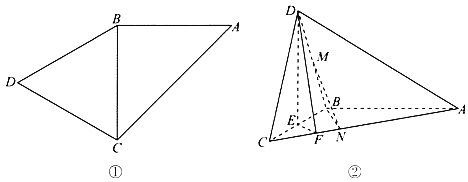
(1)試過直線MN作一平面,使它與平面DEF平行,并加以證明;
(2)記(1)中所作的平面為α,求平面α與平面BMN所成銳二面角的余弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)過![]() 作
作![]() ,交
,交![]() 于
于![]() ,連結(jié)
,連結(jié)![]() ,推導(dǎo)出
,推導(dǎo)出![]() 是
是![]() 的中點,從而
的中點,從而![]() ,由此能證明平面
,由此能證明平面![]() 平面
平面![]() .
.
(2)以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,過點
軸,過點![]() 作平面
作平面![]() 的垂線為
的垂線為![]() 軸,建立空間直角坐標(biāo)系,利用向量法能求出平面
軸,建立空間直角坐標(biāo)系,利用向量法能求出平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
(1)過N作NG∥EF,交BC于G,連結(jié)MG,則平面MNG∥平面DEF.
理由如下:
∵EF∥NG,BC的中點為E,BD的中點為M,點F、N在棱AC上,且AF=3CF,
C![]() .
.
∴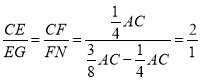 ,
,
∴G是BE的中點,
∴MG∥DE,又DE∩EF=E,MG∩NG=G,
∴平面MNG∥平面DEF.
(2)以B為原點,BC為x軸,BA為y軸,過點B作平面ABC的垂線為z軸,建立空間直角坐標(biāo)系,如下圖所示:
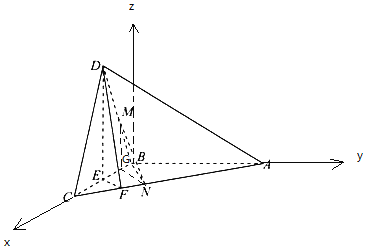
設(shè)BC=2,則B(0,0,0),D(1,0,![]() ),M(
),M(![]() ),
),
A(0,2,0),G(![]() ,0,0),N(
,0,0),N(![]() ,
,![]() ,0),
,0),
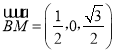 ,
,![]() ,
,![]() (0,0,
(0,0,![]() ,
,![]() ,0
,0![]() ,
,
設(shè)平面BMN的法向量![]() (x,y,z),
(x,y,z),
則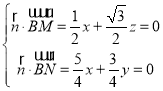 ,取
,取![]() ,得
,得![]() ,
,![]() ,﹣1
,﹣1![]() ,
,
設(shè)平面GMN的法向量![]() (x,y,z),
(x,y,z),
則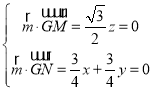 ,取x=1,得
,取x=1,得![]() (1,﹣1,0),
(1,﹣1,0),
設(shè)平面α與平面BMN所成銳二面角的平面角為θ,
則cosθ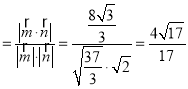 .
.
∴平面α與平面BMN所成銳二面角的余弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求證:當(dāng)![]() 時,
時,![]() 在
在![]() 上存在最小值;
上存在最小值;
(2)若![]() 是
是![]() 的零點且當(dāng)
的零點且當(dāng)![]() 時,
時,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了研究每周累計戶外暴露時間是否足夠(單位:小時)與近視發(fā)病率的關(guān)系,對某中學(xué)一年級![]() 名學(xué)生進(jìn)行不記名問卷調(diào)查,得到如下數(shù)據(jù):
名學(xué)生進(jìn)行不記名問卷調(diào)查,得到如下數(shù)據(jù):

(1)用樣本估計總體思想估計該中學(xué)一年級學(xué)生的近視率;
(2)能否認(rèn)為在犯錯誤的概率不超過![]() 的前提下認(rèn)為不足夠的戶外暴露時間與近視有關(guān)系?
的前提下認(rèn)為不足夠的戶外暴露時間與近視有關(guān)系?
附: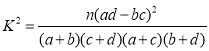 .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
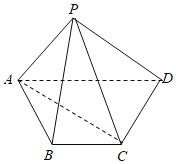
(Ⅰ)證明;AC⊥BP;
(Ⅱ)求直線AD與平面APC所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在傳染病學(xué)中,通常把從致病刺激物侵入機體或者對機體發(fā)生作用起,到機體出現(xiàn)反應(yīng)或開始呈現(xiàn)該疾病對應(yīng)的相關(guān)癥狀時止的這一階段稱為潛伏期. 一研究團(tuán)隊統(tǒng)計了某地區(qū)1000名患者的相關(guān)信息,得到如下表格:
潛伏期(單位:天) |
|
|
|
|
|
|
|
人數(shù) |
|
|
|
|
|
|
|
(1)求這1000名患者的潛伏期的樣本平均數(shù)![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(2)該傳染病的潛伏期受諸多因素的影響,為研究潛伏期與患者年齡的關(guān)系,以潛伏期是否超過6天為標(biāo)準(zhǔn)進(jìn)行分層抽樣,從上述1000名患者中抽取200人,得到如下列聯(lián)表. 請將列聯(lián)表補充完整,并根據(jù)列聯(lián)表判斷是否有![]() 的把握認(rèn)為潛伏期與患者年齡有關(guān);
的把握認(rèn)為潛伏期與患者年齡有關(guān);
潛伏期 | 潛伏期 | 總計 | |
50歲以上(含50歲) |
| ||
50歲以下 | 55 | ||
總計 | 200 |
(3)以這1000名患者的潛伏期超過6天的頻率,代替該地區(qū)1名患者潛伏期超過6天發(fā)生的概率,每名患者的潛伏期是否超過6天相互獨立. 為了深入研究,該研究團(tuán)隊隨機調(diào)查了![]() 名患者,其中潛伏期超過6天的人數(shù)最有可能(即概率最大)是多少?
名患者,其中潛伏期超過6天的人數(shù)最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=|2x﹣1|﹣|2x+1|.
(1)求不等式f(x)>1的解集.
(2)當(dāng)![]() 時,求證:4x2+4x+2>(2x+1)f(x).
時,求證:4x2+4x+2>(2x+1)f(x).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】楊輝,字謙光,南宋時期杭州人.在他1261年所著的《詳解九章算法》一書中,輯錄了如圖所示的三角形數(shù)表,稱之為“開方作法本源”圖,并說明此表引自11世紀(jì)中葉(約公元1050年)賈憲的《釋鎖算術(shù)》,并繪畫了“古法七乘方圖”.故此,楊輝三角又被稱為“賈憲三角”.楊輝三角是一個由數(shù)字排列成的三角形數(shù)表,一般形式如下:
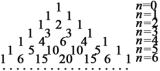
基于上述規(guī)律,可以推測,當(dāng)![]() 時,從左往右第22個數(shù)為_____________.
時,從左往右第22個數(shù)為_____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為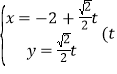 為參數(shù)
為參數(shù)![]() ,直線
,直線![]() 與曲線
與曲線![]() 分別交于
分別交于![]() 兩點.
兩點.
(1)若點![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,求
,求![]() 的值;
的值;
(2)求曲線![]() 的內(nèi)接矩形周長的最大值.
的內(nèi)接矩形周長的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() 為梯形
為梯形![]() 外一點,且
外一點,且![]() 平面
平面![]() .
.
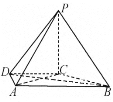
(1)求證:![]() 平面
平面![]() ;
;
(2)當(dāng)二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() 時,求這個四棱錐
時,求這個四棱錐![]() 的體積.
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com