
【題目】現有邊長分別3,4,5的三角形兩個,邊長分別4,5,![]() 的三角形四個,邊長分別為
的三角形四個,邊長分別為![]() ,4,5的三角形六個.用上述三角形為面,可以拼成______個四面體.
,4,5的三角形六個.用上述三角形為面,可以拼成______個四面體.
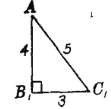
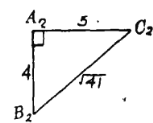
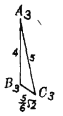
【答案】一
【解析】
如圖所示,![]() .
.
能拼成四面體的關鍵之一是兩相鄰面的交棱長相等,關鍵之二是每頂點處任兩個面角之和大于第三個面角.據題設條件知,每種三角形必須成對出現.不仿設拼成的四面體為PQRS,如圖.
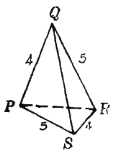
(1)若取兩個![]() 置于
置于![]() 和
和![]() 上,使
上,使![]() .
.
(i)若取兩個![]() 置于
置于![]() 和
和![]() 上,(
上,(![]() ),則P處的三個面角分別為
),則P處的三個面角分別為![]() 和
和![]() .而
.而![]() ,所以不能拼成四面體.
,所以不能拼成四面體.
(ii)若取另兩個![]() 置于
置于![]() 和
和![]() 上,(
上,(![]() )則P處的三個面角分別
)則P處的三個面角分別![]() 和
和![]() ,而
,而![]()
(![]() 可用余弦定理算之),所以也不能拼成四面體.
可用余弦定理算之),所以也不能拼成四面體.
(iii)若取兩個![]() 置于
置于![]() 和
和![]() 上(
上(![]() ),則P處的三個面角分別
),則P處的三個面角分別![]() 和
和![]() ,而
,而![]() (因為
(因為
![]() ,且
,且![]() 內
內![]() 為減函數),所以仍不能拼成.
為減函數),所以仍不能拼成.
(2)若取兩個![]() 置于
置于![]() 和
和![]() 上,使
上,使![]() .
.
(i)若取兩個![]() 另置于兩個面上(
另置于兩個面上(![]() ),由上述(1)、(iii)知不能拼成四面體.
),由上述(1)、(iii)知不能拼成四面體.
(ii)若取兩個![]() 置于另兩個面上(
置于另兩個面上(![]() ),則P處的三個面角分別
),則P處的三個面角分別![]() 和
和![]() ,而
,而![]() ,因此也不能拼成.
,因此也不能拼成.
(iii)若取另兩個![]() 置于另兩個面上(
置于另兩個面上(![]() ),則P處的三個面角分別
),則P處的三個面角分別![]() 和
和![]() ,而其中最大角
,而其中最大角![]() (因為
(因為![]() ,且
,且![]() 在
在![]() 內為增函數),即頂點處的三個面角任二個面角之和大于第三個面角成立.
內為增函數),即頂點處的三個面角任二個面角之和大于第三個面角成立.
所以,這四個三角形僅能拼成一個四面體.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)若![]() 為偶函數,求
為偶函數,求![]() 在
在![]() 上的值域;
上的值域;
(2)若![]() 的單調遞減區間為
的單調遞減區間為![]() ,求實數a構成的的集合;
,求實數a構成的的集合;
(3)若![]() 時,
時,![]() 的圖像恒在直線
的圖像恒在直線![]() 的上方,求實數a的取值范圍.
的上方,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應綠色出行,前段時間大連市在推出“共享單車”后,又推出“新能源分時租賃汽車”,其中一款新能源分時租賃汽車,每次租車收費的標準由兩部分組成:①根據行駛里程按1元/公里計費;②行駛時間不超過40分鐘時,按0.12元/分鐘計費:超出部分按0.20元/分鐘計費,己知張先生家離上班地點15公里,每天租用該款汽車上、下班各一次.由于堵車、紅路燈等因素,每次路上開車花費的時間![]() (分鐘)是一個隨機變量.現統計了100次路上開車花費時間,在各時間段內的頻數分布情況如下表所示:
(分鐘)是一個隨機變量.現統計了100次路上開車花費時間,在各時間段內的頻數分布情況如下表所示:
時間 |
|
|
|
|
頻數 | 4 | 36 | 40 | 20 |
將各時間段發生的頻率視為概率,每次路上開車花費的時間視為用車的時間,范圍為![]() 分鐘.
分鐘.
(1)寫出張先生一次租車費用![]() (元)與用車時間
(元)與用車時間![]() (分鐘)的函數關系式:
(分鐘)的函數關系式:
(2)若公司每月給900元的車補,請估計張先生每月(按24天計算)的車補是否足夠上下班租用新能源分時租賃汽車?并說明理由.(同一時段,用該區間的中點值作代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新能源汽車包括純電動汽車、增程式電動汽車、混合動力汽車、燃料電池電動汽車、氫發動機汽車、其他新能源汽車等.它是未來汽車的發展方向.一個新能源汽車制造廠引進了一條新能源汽車整車裝配流水線,這條流水線生產的新能源汽車數量![]() (輛)與創造的價值
(輛)與創造的價值![]() (萬元)之間滿足二次函數關系.已知產量為0時,創造的價值也為0;當產量為40000輛時,創造的價值達到最大6000萬元.若這家工廠希望利用這條流水線創收達到5625萬元,則它可能生產的新能源汽車數量是___________輛.
(萬元)之間滿足二次函數關系.已知產量為0時,創造的價值也為0;當產量為40000輛時,創造的價值達到最大6000萬元.若這家工廠希望利用這條流水線創收達到5625萬元,則它可能生產的新能源汽車數量是___________輛.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A,B為橢圓![]() 上的兩個動點,滿足
上的兩個動點,滿足![]() .
.
(1)求證:原點O到直線AB的距離為定值;
(2)求![]() 的最大值;
的最大值;
(3)求過點O,且分別以OA,OB為直徑的兩圓的另一個交點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
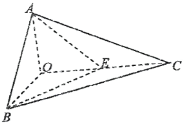
【題目】如圖,已知三棱錐O—ABC的側棱OA,OB,OC兩兩垂直,且OA=1,OB=OC=2,E是OC的中點.
(1)求異面直線BE與AC所成角的余弦值;
(2)求二面角A—BE—C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com