
【題目】已知三棱錐![]() (如圖1)的平面展開圖(如圖2)中,四邊形
(如圖1)的平面展開圖(如圖2)中,四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
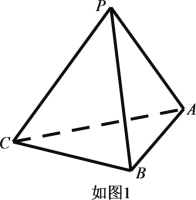

(1)證明:平面![]() 平面
平面![]() ;
;
(2)若點![]() 在棱
在棱![]() 上運動,當直線
上運動,當直線![]() 與平面
與平面![]() 所成的角最大時,求二面角
所成的角最大時,求二面角![]() 的正切值.
的正切值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)取![]() 中點
中點![]() ,連接
,連接![]() ,則
,則![]() ,由此能證明平面
,由此能證明平面![]() 平面
平面![]() (2)由
(2)由![]() ,得
,得![]() 平面
平面![]() ,從而
,從而![]() 是直線
是直線![]() 與平面
與平面![]() 所成角,且
所成角,且![]() ,進而當
,進而當![]() 最短時,即
最短時,即![]() 是
是![]() 中點時,
中點時,![]() 最大,由
最大,由![]() 平面
平面![]() ,得
,得![]() ,以
,以![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標系,利用向量法先求出二面角的余弦值,根據同角三角函數關系即可求出正切值.
軸,建立空間直角坐標系,利用向量法先求出二面角的余弦值,根據同角三角函數關系即可求出正切值.
(1 )三棱錐![]() (如圖1)的平面展開圖(如圖2)中
(如圖1)的平面展開圖(如圖2)中
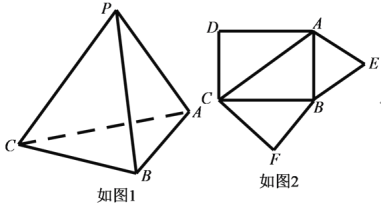
四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,
均為正三角形,
![]()
![]() ,
,
取![]() 中點
中點![]() ,連接
,連接![]() ,
,
則![]() ,
,
且![]() ,
,
![]()
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]()
(2)由(1)知![]() ,
,
![]() ,
,
![]() 平面
平面![]()
![]() 是直線
是直線![]() 與平面
與平面![]() 所成角,且
所成角,且![]() ,
,
![]() 當
當![]() 最短時,即
最短時,即![]() 是
是![]() 中點時,
中點時,![]() 最大,
最大,
由![]() 平面
平面![]() ,得
,得![]() ,
,
![]() 以
以![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立空間直角坐標系,如圖:
軸,建立空間直角坐標系,如圖:
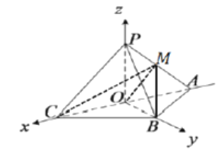
則![]() ,
,
![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則 ,取
,取![]() ,得
,得![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則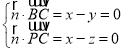 ,取
,取![]() ,得
,得![]() ,
,
設二面角![]() 的平面角為
的平面角為![]() ,
,
則![]() ,
,
所以![]() ,
,
![]() 二面角
二面角![]() 的正切值為
的正切值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某學校高一、高二、高三三個年級共有![]() 名教師,為調查他們的備課時間情況,通過分層抽樣獲得了
名教師,為調查他們的備課時間情況,通過分層抽樣獲得了![]() 名教師一周的備課時間,數據如下表(單位:小時).
名教師一周的備課時間,數據如下表(單位:小時).
高一年級 |
|
|
|
|
| |||
高二年級 |
|
|
|
|
|
|
| |
高三年級 |
|
|
|
|
|
|
|
|
(1)試估計該校高三年級的教師人數;
(2)從高一年級和高二年級抽出的教師中,各隨機選取一人,高一年級選出的人記為甲,高二年級選出的人記為乙,求該周甲的備課時間不比乙的備課時間長的概率;
(3)再從高一、高二、高三三個年級中各隨機抽取一名教師,他們該周的備課時間分別是![]() ,
, ![]() ,
, ![]() (單位:小時),這三個數據與表格中的數據構成的新樣本的平均數記為
(單位:小時),這三個數據與表格中的數據構成的新樣本的平均數記為![]() ,表格中的數據平均數記為
,表格中的數據平均數記為![]() ,試判斷
,試判斷![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司試銷一種成本單價為500元/件的新產品,規(guī)定試銷時銷售單價不低于成本單價,又不高于800元/件.經試銷調查,發(fā)現銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元/件)可近似看作一次函數
(元/件)可近似看作一次函數![]() 的關系(如圖所示).
的關系(如圖所示).

(1)由圖象,求函數![]() 的表達式;
的表達式;
(2)設公司獲得的毛利潤(毛利潤=銷售總價﹣成本總價)為![]() 元.試用銷售單價
元.試用銷售單價![]() 表示毛利潤
表示毛利潤![]() ,并求銷售單價定為多少時,該公司獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
,并求銷售單價定為多少時,該公司獲得最大毛利潤?最大毛利潤是多少?此時的銷售量是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市政府為了促進低碳環(huán)保的出行方式,從全市在冊的50000輛電動車中隨機抽取100輛,委托專業(yè)機構免費為它們進行電池性能檢測.電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進行統(tǒng)計,樣本分布如下圖.
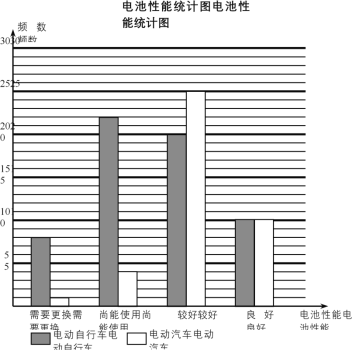
(1)從電池性能較好的電動車中,采用分層抽樣的方法隨機抽取了9輛,求再從這9輛電動車中隨機抽取2輛,至少有1輛為電動汽車的概率;
(2)為提高市民對電動車的使用熱情,市政府準備為電動車車主一次性發(fā)放補助,標準如下:
①電動自行車每輛補助300元;
②電動汽車每輛補助500元;
③對電池需要更換的電動車每輛額外補助400元.
利用樣本估計總體,試估計市政府執(zhí)行此方案的預算(單位:萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國已經成為全球最大的電商市場,但是實體店仍然是消費者接觸商品和品牌的重要渠道.某機構隨機抽取了年齡介于10歲到60歲的消費者200人,對他們的主要購物方式進行問卷調查.現對調查對象的年齡分布及主要購物方式進行統(tǒng)計,得到如下圖表:
主要購物方式 年齡階段 | 網絡平臺購物 | 實體店購物 | 總計 |
40歲以下 | 75 | ||
40歲或40歲以上 | 55 | ||
總計 |
(1)根據已知條件完成上述列聯(lián)表,并據此資料,能否在犯錯誤的概率不超過![]() 的前提下,認為消費者主要的購物方式與年齡有關?
的前提下,認為消費者主要的購物方式與年齡有關?
(2)用分層抽樣的方法從通過網絡平臺購物的消費者中隨機抽取8人,然后再從這8名消費者中抽取5名進行答謝.設抽到的消費者中40歲以下的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: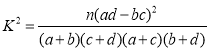 ,其中
,其中![]() .
.
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列命題是全稱量詞命題還是存在量詞命題.
(1)梯形的對角線相等;
(2)存在一個四邊形有外接圓
(3)二次函數的圖象都與x軸相交;
(4)存在一對實數x,y,使![]() 成立
成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列命題是否正確,正確的說明理由,錯誤的舉例說明.
(1)一條直線平行于一個平面,另一條直線與這個平面垂直,則這兩條直線互相垂直;
(2)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 與平面
與平面![]() 所成的二面角和平面
所成的二面角和平面![]() 與平面
與平面![]() 所成的二面角相等或互補;
所成的二面角相等或互補;
(3)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某地區(qū)2000年至2016年環(huán)境基礎設施投資額![]() (單位:億元)的折線圖.
(單位:億元)的折線圖.
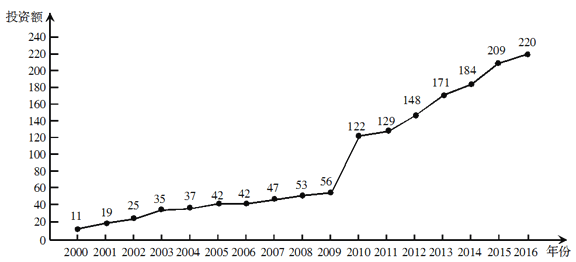
為了預測該地區(qū)2018年的環(huán)境基礎設施投資額,建立了![]() 與時間變量
與時間變量![]() 的兩個線性回歸模型.根據2000年至2016年的數據(時間變量
的兩個線性回歸模型.根據2000年至2016年的數據(時間變量![]() 的值依次為
的值依次為![]() )建立模型①:
)建立模型①:![]() ;根據2010年至2016年的數據(時間變量
;根據2010年至2016年的數據(時間變量![]() 的值依次為
的值依次為![]() )建立模型②:
)建立模型②:![]() .
.
(1)分別利用這兩個模型,求該地區(qū)2018年的環(huán)境基礎設施投資額的預測值;
(2)你認為用哪個模型得到的預測值更可靠?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年5月27日當今世界圍棋排名第一的柯潔在與![]() 的人機大戰(zhàn)中中盤棄子認輸,至此柯潔與
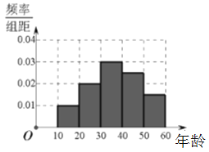
的人機大戰(zhàn)中中盤棄子認輸,至此柯潔與![]() 的三場比賽全部結束,柯潔三戰(zhàn)全負,這次人機大戰(zhàn)再次引發(fā)全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查,根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
的三場比賽全部結束,柯潔三戰(zhàn)全負,這次人機大戰(zhàn)再次引發(fā)全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查,根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.

(1)請根據已知條件完成下面![]() 列聯(lián)表,并據此資料你是否有95%的把握認為“圍棋迷”與性別有關?
列聯(lián)表,并據此資料你是否有95%的把握認為“圍棋迷”與性別有關?
非圍棋迷 | 圍棋迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)為了進一步了解“圍棋迷”的圍棋水平,從“圍棋迷”中按性別分層抽樣抽取5名學生組隊參加校際交流賽,首輪該校需派兩名學生出賽,若從5名學生中隨機抽取2人出賽,求2人恰好一男一女的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com