【題目】已知數列{an}的前n項和 
，數列{bn}的前n項和為Bn ．
（1）求數列{an}的通項公式；
（2）設 
，求數列{cn}的前n項和Cn；
（3）證明： 
．
【答案】
（1）解：當n≥2時， 
， 
，
兩式相減：an=An﹣An﹣1=2n﹣1；
當n=1時，a1=A1=1，也適合an=2n﹣1，
故數列{an}的通項公式為an=2n﹣1
（2）解：由題意知： 
，Cn=c1+c2+…+cn，
， 
，
兩式相減可得： 
，
即 
， 
， 
（3）解： 
，顯然 
，
即bn＞2，Bn=b1+b2+…+bn＞2n
另一方面， 
，
即 
， 
， 
， 
，
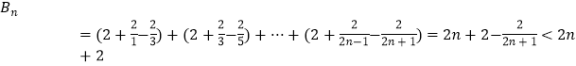即：2n＜Bn＜2n+2
【解析】（1）當n≥2時，利用an=An﹣An﹣1可得an=2n﹣1，再驗證n=1的情況，即可求得數列{an}的通項公式；（2）由題意知： ，利用錯位相減法即可求得數列{cn}的前n項和Cn；（3）利用基本不等式可得 ＞ 
，可得Bn=b1+b2+…+bn＞2n；再由bn= ，累加可 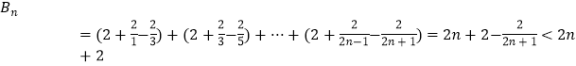， 于是可證明： 
．
【考點精析】關于本題考查的數列的通項公式，需要了解如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式才能得出正確答案．
科目：高中數學 來源： 題型：
【題目】已知數列{an}，{bn}滿足2Sn=（an+2）bn ， 其中Sn是數列{an}的前n項和．
（1）若數列{an}是首項為 
，公比為﹣ 
的等比數列，求數列{bn}的通項公式；
（2）若bn=n，a2=3，求證：數列{an}滿足an+an+2=2an+1 ， 并寫出數列{an}的通項公式；
（3）在（2）的條件下，設cn= 
， 求證：數列{cn}中的任意一項總可以表示成該數列其他兩項之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}，a1=a（a∈R），an+1= 
（n∈N*）．
（1）若數列{an}從第二項起每一項都大于1，求實數a的取值范圍；
（2）若a=﹣3，記Sn是數列{an}的前n項和，證明：Sn＜n+ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2cos（ 
﹣x）cos（x+ 
）+ 
． （Ⅰ）求函數f（x）的最小正周期和單調遞減區間；
（Ⅱ）求函數f（x）在區間[0， ]上的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，D在AB上，AD：DB=1：2，E為AC中點，CD、BE相交于點P，連結AP．設 
=x 
+y 
（x，y∈R），則x，y的值分別為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）=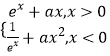 
，若函數f（x）有四個零點，則實數a的取值范圍是（ ）
A.（﹣∞，﹣e）
B.（﹣∞，﹣ 
）
C.（﹣∞，﹣ 
）
D.（﹣∞，﹣ 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
﹣axlnx（a∈R）在x=1處的切線方程為y=bx+1+ 
（b∈R）．
（1）求a，b的值；
（2）證明：f（x）＜ 
．
（3）若正實數m，n滿足mn=1，證明： 
+ 
＜2（m+n）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次購物抽獎活動中，假設某10張券中有一等獎券1張，可獲價值50元的獎品；有二等獎券3張，每張可獲價值10元的獎品；其余6張沒有獎，某顧客從此10張券中任抽2張，求：
（Ⅰ）該顧客中獎的概率；
（Ⅱ）該顧客獲得的獎品總價值ξ（元）的概率分布列和期望Eξ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=cos（2x﹣ 
）+2cos2x，將函數y=f（x）的圖象向右平移 
個單位，得到函數y=g（x）的圖象，則函數y=g（x）圖象的一個對稱中心是（ ）
A.（﹣ 
，1）
B.（﹣ 
，1）
C.（ ，1）
D.（ 
，0）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com