..(本題滿分12分) 本題共有2個小題,第1小題滿分6分,第2小題滿分6分.
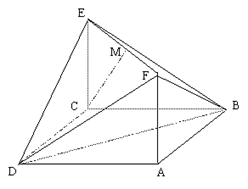
(理)如圖,已知矩形
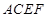
的邊

與正方形

所在平面垂直,
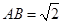
,
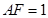
,
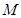
是線段
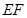
的中點。
(1)求證:
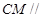
平面
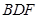
;
(2)求二面角
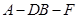
的大小。
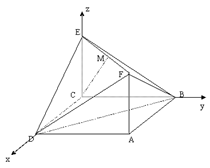
(理)解:(1)建立如圖所示的空間直角坐標系,則

……………… 2分
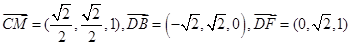
設平面

的一個法向量為

,則
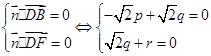
取

,得平面

的一個法向量為
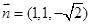
,…………………………6分
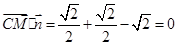
,
所以
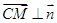
,又因為直線

不在平面

內,所以
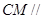
平面

。
……………………………………………6分
(2)由(1)知平面

的一個法向量為
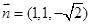
,而平面

的一個法向量為
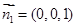
,

……………………………… 11分
所以向量
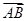
與向量
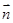
的夾角
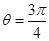
,從圖中可以看出二面角

為銳二面角,所以所求二面角

的大小是

。 …………… 12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
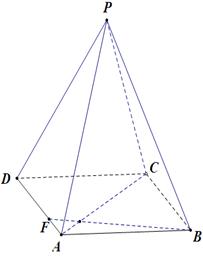
如圖所示,正四棱錐
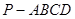
中,AB=1,側棱
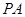
與底面
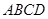
所成角的正切值為
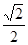
.
(1)求二面角P-CD-A的大小.
(2)設點F在AD上,
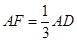
,求點A到平面PB

F的距離.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,正方體

中,

的中點為

,

的中點為

,則異
面直線

與

所成的是( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
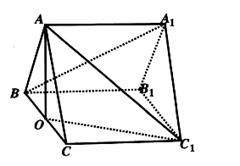
已知三棱柱
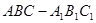
,底面
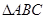
為正三角形,
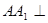
平面
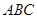

,
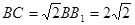
,
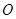
為
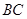
中點.
(Ⅰ)求證:
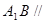
平面
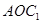
;
(Ⅱ)求直線
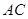
與平面
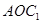
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
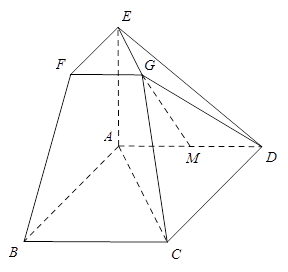
在如圖所示的幾何體中,四邊形
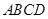
為平行四邊形,
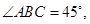
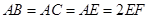
,
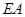
⊥平面
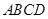
,
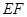
∥
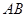
,
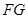
∥
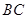
,
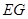
∥
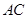
.
(1)若
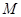
是線段
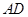
的中點,求證:
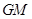
∥平面
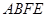
;
(2)求二面角
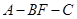
的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知三條不重合的直線
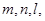
兩個不重合的平面
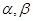
,給出下列四個命題:
①若
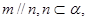
則
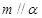
;
②若
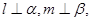
且
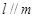
則
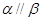
;
③若
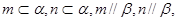
則
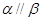
;
④若
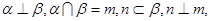
則
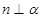
. 其中真命題是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
四棱錐
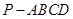
中,

⊥底面

,

∥

,

(1)求證:
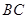
⊥平面

;
(2)求二面角

的平面角的余弦值;
(3)求點
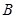
到平面

的距離。

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知長方體的全面積11,十二條棱的長之和為24,則這個長方體的一條對角線的長為( )
A.2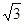 | B.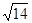 | C.5 | D.6 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
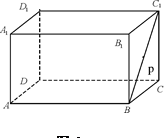
如圖4,點
P在長方體
ABCD-
A1B1C1D1的面對角線
BC1(線段
BC1)上運動,給出下列四個命題:
①直線
AD與直線
B1P為異面直線;
②恒有
A1P∥面
ACD1;
③三棱錐
A-
D1PC的體積為定值;
④當且僅當長方體各棱長都相等時,面
PDB1⊥面
ACD1.
其中所有正確命題的序號是
查看答案和解析>>

 的邊
的邊 與正方形
與正方形 所在平面垂直,
所在平面垂直,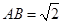 ,
,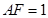 ,
,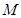 是線段
是線段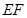 的中點。
的中點。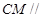 平面
平面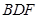 ;
;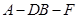 的大小。
的大小。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案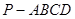 中,AB=1,側棱
中,AB=1,側棱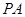 與底面
與底面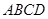 所成角的正切值為
所成角的正切值為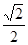 .
.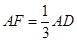 ,求點A到平面PB
,求點A到平面PB F的距離.
F的距離.

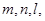 兩個不重合的平面
兩個不重合的平面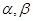 ,給出下列四個命題:
,給出下列四個命題: 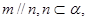 則
則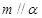 ;
;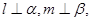 且
且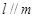 則
則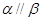 ;
;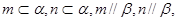 則
則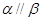 ;
;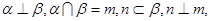 則
則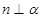 . 其中真命題是 ( )
. 其中真命題是 ( )