
【題目】定義:若對定義域內任意x,都有![]() (a為正常數),則稱函數
(a為正常數),則稱函數![]() 為“a距”增函數.
為“a距”增函數.
(1)若![]() ,
,![]() (0,
(0,![]() ),試判斷
),試判斷![]() 是否為“1距”增函數,并說明理由;
是否為“1距”增函數,并說明理由;
(2)若![]() ,
,![]() R是“a距”增函數,求a的取值范圍;
R是“a距”增函數,求a的取值范圍;
(3)若![]() ,
,![]() (﹣1,
(﹣1,![]() ),其中k
),其中k![]() R,且為“2距”增函數,求
R,且為“2距”增函數,求![]() 的最小值.
的最小值.
【答案】(1)見解析; (2)![]() ; (3)
; (3)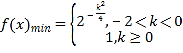 .
.
【解析】
(1)利用“1距”增函數的定義證明![]() 即可;(2)由“a距”增函數的定義得到
即可;(2)由“a距”增函數的定義得到![]() 在
在![]() 上恒成立,求出a的取值范圍即可;(3)由
上恒成立,求出a的取值范圍即可;(3)由![]() 為“2距”增函數可得到
為“2距”增函數可得到![]() 在
在![]() 恒成立,從而得到
恒成立,從而得到![]() 恒成立,分類討論可得到
恒成立,分類討論可得到![]() 的取值范圍,再由
的取值范圍,再由![]() ,可討論出
,可討論出![]() 的最小值。
的最小值。
(1)任意![]() ,
,![]() ,
,
因為![]() ,
,![]() , 所以
, 所以![]() ,所以
,所以![]() ,即
,即![]() 是“1距”增函數。
是“1距”增函數。
(2)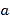 .
.
因為![]() 是“
是“![]() 距”增函數,所以
距”增函數,所以![]() 恒成立,
恒成立,
因為![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,解得
,解得![]() ,因為
,因為![]() ,所以
,所以![]() .
.
(3)因為![]() ,
,![]() ,且為“2距”增函數,
,且為“2距”增函數,
所以![]() 時,
時,![]() 恒成立,
恒成立,
即![]() 時,
時,![]() 恒成立,
恒成立,
所以![]() ,
,
當![]() 時,
時,![]() ,即
,即![]() 恒成立,
恒成立,
所以![]() , 得
, 得![]() ;
;
當![]() 時,
時,![]() ,
,
得![]() 恒成立,
恒成立,
所以![]() ,得
,得![]() ,
,
綜上所述,得![]() .
.
又![]() ,
,
因為![]() ,所以
,所以![]() ,
,
當![]() 時,若
時,若![]() ,
,![]() 取最小值為
取最小值為![]() ;
;
當![]() 時,若
時,若![]() ,
,![]() 取最小值.
取最小值.
因為![]() 在R上是單調遞增函數,
在R上是單調遞增函數,
所以當![]() ,
,![]() 的最小值為
的最小值為![]() ;當
;當![]() 時
時![]() 的最小值為
的最小值為![]() ,
,
即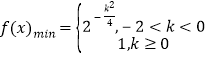 .
.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
【題目】已知集合A是函數y=lg(20﹣8x﹣x2)的定義域,集合B是不等式x2﹣2x+1﹣a2≥0(a>0)的解集,p:x∈A,q:x∈B.
(1)若A∩B=,求實數a的取值范圍;
(2)若¬p是q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現安排甲、乙、丙、丁、戊5名同學參加廈門市華僑博物院志愿者服務活動,每人從事禮儀、導游、翻譯、講解四項工作之一,每項工作至少有一人參加. 甲、乙不會導游但能從事其他三項工作,丙、丁、戊都能勝任四項工作,則不同安排方案的種數是____________.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的一段圖象如圖5所示:將
的一段圖象如圖5所示:將![]() 的圖像向右平移
的圖像向右平移![]() 個單位,可得到函數
個單位,可得到函數![]() 的圖象,且圖像關于原點對稱,
的圖象,且圖像關于原點對稱,

(1)求![]() 的值;
的值;
(2)求![]() 的最小值,并寫出
的最小值,并寫出![]() 的表達式;
的表達式;
(3)若關于![]() 的函數
的函數![]() 在區間
在區間![]() 上最小值為
上最小值為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 線性回歸直線![]() 至少經過其樣本數據點中的一個點
至少經過其樣本數據點中的一個點
B. 在統計學中,獨立性檢驗是檢驗兩個分類變量是否有關系的一種統計方法
C. 在回歸分析中,相關指數![]() 越大,模擬的效果越好
越大,模擬的效果越好
D. 在殘差圖中,殘差分布的帶狀區域的寬度越狹窄,其模擬的效果越好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將邊長為1的正方形![]() 沿對角線
沿對角線![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,在折起后形成的三棱錐
,在折起后形成的三棱錐![]() 中,給出下列三種說法:
中,給出下列三種說法:
①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③三棱錐
;③三棱錐![]() 的體積是
的體積是![]() .
.
其中正確的序號是__________(寫出所有正確說法的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|2x+1|+|x﹣a|,a∈R. (Ⅰ)當a=2時,求不等式f(x)<4的解集.
(Ⅱ)當a< ![]() 時,對于x∈(﹣∞,﹣
時,對于x∈(﹣∞,﹣ ![]() ],都有f(x)+x≥3成立,求a的取值范圍.
],都有f(x)+x≥3成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com