
【題目】如圖,已知![]() 是上、下底邊長分別為2和6,高為
是上、下底邊長分別為2和6,高為![]() 的等腰梯形,將它沿對稱軸
的等腰梯形,將它沿對稱軸![]() 折疊,使二面角
折疊,使二面角![]() 為直二面角.
為直二面角.

(1)證明: ![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)見解析;(2)![]()
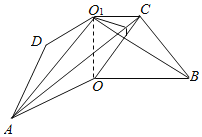
【解析】試題分析:(1)由OA⊥OO1,OB⊥OO1,知∠AOB是所折成的直二面角的平面角,從而OA⊥OB,進而推導出OC⊥BO1,由此能證明AC⊥BO1.
(2)推導出BO1⊥平面AOC,設OC∩O1B=E,過點E作EF⊥AC于F,連結O1F,則∠O1FE是二面角O﹣AC﹣O1的平面角,由此能求出二面角O﹣AC﹣O1的余弦值.
試題解析:
證明:(1)由題設知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB
從而AO⊥平面OBCO1,
OC是AC在面OBCO1內的射影
因為tan∠OO1A=![]() =
=![]() ,tan∠O1OC=
,tan∠O1OC=![]() =
=![]() ,
,
所以∠OO1B=60°,∠O1OC=30°,
從而OC⊥BO1
由三垂線定理得AC⊥BO1.
解:(2)由(1)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC
設OC∩O1B=E,過點E作EF⊥AC于F,連結O1F(如圖),
則EF是O1F在平面AOC 內的射影,
由三垂線定理得O1F⊥AC
所以∠O1FE是二面角O﹣AC﹣O1的平面角
由題設知OA=3,OO1=![]() ,O1C=1,
,O1C=1,
所以![]() =2
=2![]() ,AC=
,AC=![]() =
=![]() ,
,
從而![]() =
=![]() ,
,
又O1E=OO1sin30°=![]() ,
,
所以sin∠O1FE=![]() =
=![]() ,
,
∴二面角O﹣AC﹣O1的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知首項為 ![]() 的等比數列
的等比數列 ![]() 是遞減數列,且
是遞減數列,且 ![]() ,
, ![]() ,
, ![]() 成等差數列;數列
成等差數列;數列 ![]() 的前
的前 ![]() 項和為
項和為 ![]() ,且
,且 ![]() ,
, ![]()
(Ⅰ)求數列 ![]() ,
, ![]() 的通項公式;
的通項公式;
(Ⅱ)已知 ![]() ,求數列
,求數列 ![]() 的前
的前 ![]() 項和
項和 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,動點P從單位正方形ABCD頂點A開始,順次經B、C、D繞邊界一周,當![]() 表示點P的行程,
表示點P的行程, ![]() 表示PA之長時,求y關于x的解析式,并求
表示PA之長時,求y關于x的解析式,并求![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:關于x的方程x2﹣ax+4=0有實根;命題q:關于x的函數y=2x2+ax+4在[3,+∞)上是增函數,若p∧q是真命題,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設直線l的參數方程為  (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=4cosθ.
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=4cosθ.
(1)把曲線C的極坐標方程化為直角坐標方程;
(2)設直線l與曲線C交于M,N兩點,點A(1,0),求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com