
【題目】若![]() 是兩條不同的直線,
是兩條不同的直線, ![]() 是三個不同的平面,下面說法正確的是( )
是三個不同的平面,下面說法正確的是( )
A. 若![]() ,則
,則![]() B. 若
B. 若![]() ,則
,則![]()
C. 若![]() ,則
,則![]() D. 若
D. 若![]() ,則
,則![]()
【答案】B
【解析】若![]() ,則
,則![]() 與
與![]() 平行,相交或
平行,相交或![]() ,故
,故![]() 不正確;若
不正確;若![]() ,則
,則![]() ,
, ![]() ,根據線面平行的性質在
,根據線面平行的性質在![]() 內至少存在一條直線
內至少存在一條直線![]() 與
與![]() 平行,根據線面垂直的判定:如果兩條平行線中的一條垂直這個平面,那么另一條也垂直于該平面,
平行,根據線面垂直的判定:如果兩條平行線中的一條垂直這個平面,那么另一條也垂直于該平面, ![]()
![]() ,可得
,可得![]() ,故
,故![]() 正確;若
正確;若![]()
![]() ,
, ![]() ,則
,則![]() 或
或![]() 與
與![]() 相交,故
相交,故![]() 不正確;若
不正確;若![]() ,則
,則![]() 與
與![]() 相交或平行,故
相交或平行,故![]() 不正確,故選B.
不正確,故選B.
【方法點晴】本題主要考查線面平行的判定與性質、面面垂直的性質及線面垂直的判定,屬于難題.空間直線、平面平行或垂直等位置關系命題的真假判斷,常采用畫圖(尤其是畫長方體)、現實實物判斷法(如墻角、桌面等)、排除篩選法等;另外,若原命題不太容易判斷真假,可以考慮它的逆否命題,判斷它的逆否命題真假,原命題與逆否命題等價.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】如圖, ![]() 是
是![]() 直徑,
直徑, ![]() 所在的平面,
所在的平面, ![]() 是圓周上不同于
是圓周上不同于![]() 的動點.
的動點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且當二面角
,且當二面角![]() 的正切值為
的正切值為![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在實數集R中定義一種運算“*”,對任意給定的a,b∈R,a*b為唯一確定的實數,且具有性質: ⑴對任意a,b∈R,a*b=b*a;(2)對任意a∈R,a*0=a;(3)對任意a,b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.關于函數f(x)=(3x)* ![]() 的性質,有如下說法:
的性質,有如下說法:
①函數f(x)的最小值為3;
②函數f(x)為奇函數;
③函數f(x)的單調遞增區間為(﹣∞,﹣ ![]() ),(
),( ![]() ,+∞).
,+∞).
其中所有正確說法的個數為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 是邊長為2的正方形,
是邊長為2的正方形, ![]() 分別為線段
分別為線段![]() ,
, ![]() 的中點.
的中點.
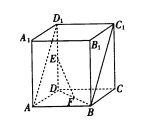
(1)求證: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面積為
的外接球的表面積為![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]()
![]() 在某一周期內的圖象時,列表并填入了部分數據,如下表:
在某一周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(Ⅰ)請將上表數據補充完整,函數![]() 的解析式
的解析式![]() (直接寫出結果即可)
(直接寫出結果即可)
(Ⅱ)求函數![]() 的單調遞增區間;/span>
的單調遞增區間;/span>
(Ⅲ)求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com