【題目】
已知函數
，其中
是常數.
(Ⅰ)當
時，求曲線
在點
處的切線方程；
（Ⅱ）若存在實數
，使得關于
的方程
在
上有兩個不相等的實數根，求的取值范圍.
【答案】（Ⅰ）
（Ⅱ）
【解析】
（Ⅰ）當a＝1時，f（1）＝e，f′（1）＝4e，由點斜式可求得y＝f（x）在點（1，f（1））處的切線方程；
（Ⅱ） 令f′（x）＝ex[x2+（a+2）x）]＝0，可解得x＝﹣（a+2）或x＝0，對﹣（a+2）與0的大小關系分類討論，可求得關于x的方程f（x）＝k在[0，+∞）上有兩個不相等的實數根的k的取值范圍．
解：(Ⅰ)由
可得
.
當
時,
,
.
所以 曲線
在點
處的切線方程為
，
即
（Ⅱ） 令
，
解得
或
當
，即
時，在區間
上，
，所以
是上的增函數.
所以 方程
在上不可能有兩個不相等的實數根.
當
，即
時，
隨
的變化情況如下表
|
|
|
|
|
|
|
|
|
|
|
| ↘ |
| ↗ |
由上表可知函數在上的最小值為
.
因為 函數是
上的減函數，是
上的增函數，
且當
時，有
.
所以 要使方程在上有兩個不相等的實數根，
的取值范圍必須是
.
科目：高中數學 來源： 題型：
【題目】已知定義域為
的函數
在
上有最大值1，設
．
（1）求
的值；
（2）若不等式
在
上恒成立，求實數
的取值范圍；
（3）若函數
有三個不同的零點，求實數的取值范圍（
為自然對數的底數）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知拋物線
的頂點為
,與
軸的交點為
,則直線
稱為拋物線
的伴隨直線.
(1)求拋物線
的伴隨直線的表達式;
(2)已知拋物線
的伴隨直線為
,且該拋物線與
軸有兩個不同的公共點,求
的取值范圍.
(3)已知
,若拋物線的伴隨直線為
,且該拋物線與線段
恰有1個公共點,求的取值范圍(直接寫出答案即可)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為雙曲線
的左、右焦點，過
作垂直于
軸的直線，并在軸上方交雙曲線于點
，且
.
（1）求雙曲線
的方程；
（2）過雙曲線上一點
作兩條漸近線的垂線，垂足分別是
和
，試求
的值；
（3）過圓
上任意一點
作切線
交雙曲線于
兩個不同點，
中點為
，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高一年級6個班級去蘇州、黃山、廈門三個地方修學旅行，每個城市至少有一個班前去，其中1班和2班不能去同一個地方，則共有_________種不同分配方法？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某互聯網公司為了確定下一季度的前期廣告投入計劃，收集了近
個月廣告投入量
（單位：萬元）和收益
（單位：萬元）的數據如下表：
月份 |
|
|
|
|
|
|
廣告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他們分別用兩種模型①
，②
分別進行擬合，得到相應的回歸方程并進行殘差分析，得到如圖所示的殘差圖及一些統計量的值：
|
|
|
|
|
|
|
|
（Ⅰ）根據殘差圖，比較模型①，②的擬合效果，應選擇哪個模型？并說明理由；
（Ⅱ）殘差絕對值大于
的數據被認為是異常數據，需要剔除：
（ⅰ）剔除異常數據后求出（Ⅰ）中所選模型的回歸方程
（ⅱ）若廣告投入量
時，該模型收益的預報值是多少？
附：對于一組數據
，
，……，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
，
.
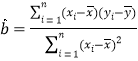
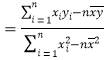查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】據不完全統計，某廠的生產原料耗費
（單位：百萬元）與銷售額
（單位：百萬元）如下：
| 2 | 4 | 6 | 8 |
| 30 | 40 | 50 | 70 |
變量、為線性相關關系.
（1）求線性回歸方程必過的點；
（2）求線性回歸方程；
（3）若實際銷售額要求不少于
百萬元，則原材料耗費至少要多少百萬元。
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P—ABCD中，底面ABCD是正方形，側棱PD⊥底面ABCD，PD=DC，E、F分別是PC、AD中點，
(1)求證：DE//平面PFB；
(2)求PB與面PCD所成角的正切值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
