
【題目】已知E,F分別是棱長為1的正方體ABCD﹣A1B1C1D1的棱BC,CC1的中點,則截面AEFD1與底面ABCD所成二面角的正弦值是 .
【答案】![]()
【解析】解:以D為原點,DA為x軸,DC為y軸,DD1為z軸,建立空間直角坐標系,
A(1,0,0),E( ![]() ,1,0),F(0,1,
,1,0),F(0,1, ![]() ),
),![]() =(﹣
=(﹣ ![]() ,1,0),
,1,0), ![]() =(﹣1,1,
=(﹣1,1, ![]() ),
),
設平面AEFD1的法向量 ![]() =(x,y,z),
=(x,y,z),
則  ,取x=2,得
,取x=2,得 ![]() =(2,1,2),
=(2,1,2),
平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
截面AEFD1與底面ABCD所成二面角為θ,
cosθ= ![]() =
= ![]() ,
,
∴sinθ= ![]() =
= ![]() .
.
∴截面AEFD1與底面ABCD所成二面角的正弦值是 ![]() .
.
故答案為: ![]() .
.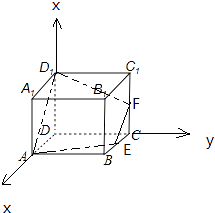
以D為原點,DA為x軸,DC為y軸,DD1為z軸,建立空間直角坐標系,利用向量法能求出截面AEFD1與底面ABCD所成二面角的正弦值.


科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1中,側棱AA1⊥平面ABC.若AB=AC=AA1=1,BC= ![]() ,則異面直線A1C與B1C1所成的角為( )
,則異面直線A1C與B1C1所成的角為( ) 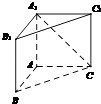
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 為f(x)的零點,x=
為f(x)的零點,x= ![]() 為y=f(x)圖象的對稱軸,且f(x)在(
為y=f(x)圖象的對稱軸,且f(x)在( ![]() ,
, ![]() )單調,則ω的最大值為 .
)單調,則ω的最大值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD中邊長為1,P、Q分別為BC、CD上的點,△CPQ周長為2. 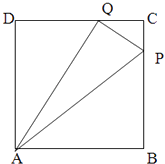
(1)求PQ的最小值;
(2)試探究求∠PAQ是否為定值,若是給出證明;不是說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線實軸長為6,一條漸近線方程為4x﹣3y=0.過雙曲線的右焦點F作傾斜角為 ![]() 的直線交雙曲線于A、B兩點
的直線交雙曲線于A、B兩點
(1)求雙曲線的方程;
(2)求線段AB的中點C到焦點F的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側棱垂直于底面,底面是邊長為2的正三角形,側棱長為3,則BB1與平面AB1C1所成的角是( )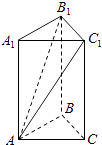
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各命題中不正確的是( )
A.函數f(x)=ax+1(a>0,a≠1)的圖象過定點(﹣1,1)
B.函數 ![]() 在[0,+∞)上是增函數
在[0,+∞)上是增函數
C.函數f(x)=logax(a>0,a≠1)在(0,+∞)上是增函數
D.函數f(x)=x2+4x+2在(0,+∞)上是增函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣e﹣x+4sin3x+1,x∈(﹣1,1),若f(1﹣a)+f(1﹣a2)>2成立,則實數a的取值范圍是( )
A.(﹣2,1)
B.(0,1)
C.![]()
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com