
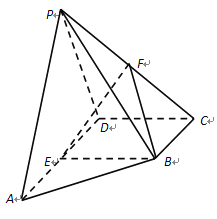
【題目】在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 底面
底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 的中點(diǎn)。
的中點(diǎn)。
(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)見(jiàn)證明;(2)![]()
【解析】
(1)利用面外線與面內(nèi)線平行證明面外線平行于平面。
(2)建立空間直角坐標(biāo)系,利用兩個(gè)半平面的法向量的夾角余弦值,來(lái)求二面角的平面角的余弦值,或用幾何法找到二面角的平面角來(lái)求余弦值。
(1)連接![]() 交
交![]() 于
于![]() ,并連接
,并連接![]() ,
,![]() ,
,

![]() ,
,![]() ,
,![]() 為
為![]() 中點(diǎn),
中點(diǎn),![]() ,且
,且![]() ,
,
![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,
![]() 為
為![]() 中點(diǎn),又
中點(diǎn),又![]() 為
為![]() 中點(diǎn),
中點(diǎn),![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)〖解法1〗(向量法)連接![]() ,由E為AD的中點(diǎn)及
,由E為AD的中點(diǎn)及![]() ,
,

得![]() 則
則![]() ,∵側(cè)面
,∵側(cè)面![]() 底面
底面![]() ,且交于
,且交于![]() ,
,
∴![]() 面
面![]() ,
,
如圖所示,以E為原點(diǎn),EA、EB、EP分別為
x、y、z軸建立空間直角坐標(biāo)系,
則![]() ,
,![]() ,
,![]() ,C
,C![]() .
.
∵![]() 為
為![]() 的中點(diǎn),∴F
的中點(diǎn),∴F![]()
∴![]() ,
,
設(shè)平面EBF法向量為![]() ,則
,則 ,
,
取![]() ,
,
平面EBA法向量可取:![]() ,
,
設(shè)二面角F-BE-A的大小為![]() ,顯然
,顯然![]() 為鈍角,
為鈍角,
∴![]() ,
,
∴二面角F-BE-A的余弦值為![]()
(2)〖解法2〗(幾何法1)連接![]() ,
,

由E為AD的中點(diǎn)及![]() ,
,
得![]() ∵
∵![]() ,
,![]()
取![]() 中點(diǎn)
中點(diǎn)![]() ,連
,連![]() ,
,![]() ,
,![]() ,
,
![]() 側(cè)面
側(cè)面![]() 底面
底面![]() ,且交于
,且交于![]() ,
,![]() ,
,
∴![]() 面
面![]()
∵ ![]() 面
面![]()
![]() 面
面![]()
∴![]()
∵![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 的中點(diǎn)
的中點(diǎn)
![]() ,
,![]()
∴![]()
∴∠MEA為二面角F-BE-A的平面角
在![]() 中,
中,![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]()
∴在![]() 中,由余弦定理得cos∠MEA
中,由余弦定理得cos∠MEA![]() ,
,
所以二面角F-BE-A的余弦值為![]() .
.
(2)〖解法3〗(幾何法2)連接![]() ,由E為AD的中點(diǎn)及
,由E為AD的中點(diǎn)及![]() ,
,
得![]() 側(cè)面
側(cè)面![]() 底面
底面![]() ,∴
,∴![]() 面
面![]() ,
,

∵![]() ,
,![]()
連![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,則
,則![]() 為
為![]() 中點(diǎn),連
中點(diǎn),連![]() ,
,![]() ,
,![]() ,
,
∵![]() 為
為![]() 的中點(diǎn),∴
的中點(diǎn),∴![]() ,
,![]() 面
面![]() ,
,
又![]() ,∴
,∴![]() ∴
∴ ![]()
∴∠FNQ為二面角F-BE-A的平面角的補(bǔ)角
在![]() 中,
中,![]() ,
,
由勾股定理得![]()
∴cos∠FNQ![]() ,
,
所以二面角F-BE-A的余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】焦距為![]() 的橢圓
的橢圓![]() (
(![]() ),如果滿足“
),如果滿足“![]() ”,則稱此橢圓為“等差橢圓”.
”,則稱此橢圓為“等差橢圓”.
(1)如果橢圓![]() (
(![]() )是“等差橢圓”,求
)是“等差橢圓”,求![]() 的值;
的值;
(2)如果橢圓![]() (
(![]() )是“等差橢圓”,過(guò)
)是“等差橢圓”,過(guò)![]() 作直線
作直線![]() 與此“等差橢圓”只有一個(gè)公共點(diǎn),求此直線的斜率;
與此“等差橢圓”只有一個(gè)公共點(diǎn),求此直線的斜率;
(3)橢圓![]() (
(![]() )是“等差橢圓”,如果焦距為12,求此“等差橢圓”的方程;
)是“等差橢圓”,如果焦距為12,求此“等差橢圓”的方程;
(4)對(duì)于焦距為12的“等差橢圓”,點(diǎn)![]() 為橢圓短軸的上頂點(diǎn),
為橢圓短軸的上頂點(diǎn),![]() 為橢圓上異于
為橢圓上異于![]() 點(diǎn)的任一點(diǎn),
點(diǎn)的任一點(diǎn),![]() 為
為![]() 關(guān)于原點(diǎn)
關(guān)于原點(diǎn)![]() 的對(duì)稱點(diǎn)(
的對(duì)稱點(diǎn)(![]() 也異于
也異于![]() ),直線
),直線![]()
![]() 分別與
分別與![]() 軸交于
軸交于![]()
![]() 兩點(diǎn),判斷以線段
兩點(diǎn),判斷以線段![]() 為直徑的圓是否過(guò)定點(diǎn)?說(shuō)明理由.
為直徑的圓是否過(guò)定點(diǎn)?說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=sin(2ωx+![]() )+sin(2ωx-
)+sin(2ωx-![]() )+2cos2ωx,其中ω>0,且函數(shù)f(x)的最小正周期為π
)+2cos2ωx,其中ω>0,且函數(shù)f(x)的最小正周期為π
(1)求ω的值;
(2)求f(x)的單調(diào)增區(qū)間
(3)若函數(shù)g(x)=f(x)-a在區(qū)間[-![]() ,
,![]() ]上有兩個(gè)零點(diǎn),求實(shí)數(shù)a的取值范圍.
]上有兩個(gè)零點(diǎn),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】高中生在被問(wèn)及“家,朋友聚集的地方,個(gè)人空間”三個(gè)場(chǎng)所中“感到最幸福的場(chǎng)所在哪里?”這個(gè)問(wèn)題時(shí),從中國(guó)某城市的高中生中,隨機(jī)抽取了55人,從美國(guó)某城市的高中生中隨機(jī)抽取了45人進(jìn)行答題.中國(guó)高中生答題情況是:選擇家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、個(gè)人空間占
、個(gè)人空間占![]() .美國(guó)高中生答題情況是:朋友聚集的地方占
.美國(guó)高中生答題情況是:朋友聚集的地方占![]() 、家占
、家占![]() 、個(gè)人空間占
、個(gè)人空間占![]() .如下表:
.如下表:
在家里最幸福 | 在其它場(chǎng)所幸福 | 合計(jì) | |
中國(guó)高中生 | |||
美國(guó)高中生 | |||
合計(jì) |
(Ⅰ)請(qǐng)將![]() 列聯(lián)表補(bǔ)充完整;試判斷能否有
列聯(lián)表補(bǔ)充完整;試判斷能否有![]() 的把握認(rèn)為“戀家”與否與國(guó)別有關(guān);
的把握認(rèn)為“戀家”與否與國(guó)別有關(guān);
(Ⅱ)從被調(diào)查的不“戀家”的美國(guó)學(xué)生中,用分層抽樣的方法選出4人接受進(jìn)一步調(diào)查,再?gòu)?/span>4人中隨機(jī)抽取2人到中國(guó)交流學(xué)習(xí),求2人中含有在“個(gè)人空間”感到幸福的學(xué)生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】[選修4-4:坐標(biāo)系與參數(shù)方程]
在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以原點(diǎn)
為參數(shù)),以原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫(xiě)出曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知點(diǎn)![]() 是曲線
是曲線![]() 上的動(dòng)點(diǎn),求點(diǎn)
上的動(dòng)點(diǎn),求點(diǎn)![]() 到曲線
到曲線![]() 的最小距離.
的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某醫(yī)療器械公司在全國(guó)共有![]() 個(gè)銷(xiāo)售點(diǎn),總公司每年會(huì)根據(jù)每個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)量進(jìn)行評(píng)價(jià)分析.規(guī)定每個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)售任務(wù)為一萬(wàn)四千臺(tái)器械.根據(jù)這
個(gè)銷(xiāo)售點(diǎn),總公司每年會(huì)根據(jù)每個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)量進(jìn)行評(píng)價(jià)分析.規(guī)定每個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)售任務(wù)為一萬(wàn)四千臺(tái)器械.根據(jù)這![]() 個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)量繪制出如下的頻率分布直方圖.
個(gè)銷(xiāo)售點(diǎn)的年銷(xiāo)量繪制出如下的頻率分布直方圖.
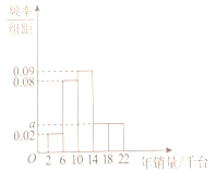
(1)完成年銷(xiāo)售任務(wù)的銷(xiāo)售點(diǎn)有多少個(gè)?
(2)若用分層抽樣的方法從這![]() 個(gè)銷(xiāo)售點(diǎn)中抽取容量為
個(gè)銷(xiāo)售點(diǎn)中抽取容量為![]() 的樣本,求該五組
的樣本,求該五組![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(單位:千臺(tái))中每組分別應(yīng)抽取的銷(xiāo)售點(diǎn)數(shù)量.
,(單位:千臺(tái))中每組分別應(yīng)抽取的銷(xiāo)售點(diǎn)數(shù)量.
(3)在(2)的條件下,從前兩組![]() ,
,![]() 中的銷(xiāo)售點(diǎn)隨機(jī)選取
中的銷(xiāo)售點(diǎn)隨機(jī)選取![]() 個(gè),記這
個(gè),記這![]() 個(gè)銷(xiāo)售點(diǎn)在
個(gè)銷(xiāo)售點(diǎn)在![]() 中的個(gè)數(shù)為
中的個(gè)數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為推動(dòng)文明城市創(chuàng)建,提升城市整體形象,2018年12月30日鹽城市人民政府出臺(tái)了《鹽城市停車(chē)管理辦法》,2019年3月1日起施行.這項(xiàng)工作有利于市民養(yǎng)成良好的停車(chē)習(xí)慣,幫助他們樹(shù)立綠色出行的意識(shí),受到了廣大市民的一致好評(píng).現(xiàn)從某單位隨機(jī)抽取80名職工,統(tǒng)計(jì)了他們一周內(nèi)路邊停車(chē)的時(shí)間![]() (單位:小時(shí)),整理得到數(shù)據(jù)分組及頻率分布直方圖如下:
(單位:小時(shí)),整理得到數(shù)據(jù)分組及頻率分布直方圖如下:

組號(hào) | 分組 | 頻數(shù) |
1 |
| 6 |
2 |
| 8 |
3 |
| 22 |
4 |
| 28 |
5 |
| 12 |
6 |
| 4 |
(1)從該單位隨機(jī)選取一名職工,試計(jì)算這名職工一周內(nèi)路邊停車(chē)的時(shí)間少于8小時(shí)的頻率;
(2)求頻率分布直方圖中![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的兩個(gè)焦點(diǎn)
的兩個(gè)焦點(diǎn)![]() ,
,![]() ,且橢圓過(guò)點(diǎn)
,且橢圓過(guò)點(diǎn)![]() ,
,![]() ,且
,且![]() 是橢圓上位于第一象限的點(diǎn),且
是橢圓上位于第一象限的點(diǎn),且![]() 的面積
的面積![]() .
.
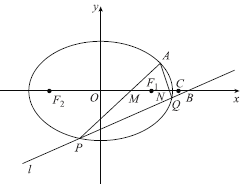
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)過(guò)點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() ,直線
,直線![]() ,
,![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() ,則
,則![]() 是否為定值,如果是定值,求出這個(gè)定值,如果不是請(qǐng)說(shuō)明理由.
是否為定值,如果是定值,求出這個(gè)定值,如果不是請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com