
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,
,![]() ,且橢圓過點
,且橢圓過點![]() ,
,![]() ,且
,且![]() 是橢圓上位于第一象限的點,且
是橢圓上位于第一象限的點,且![]() 的面積
的面積![]() .
.
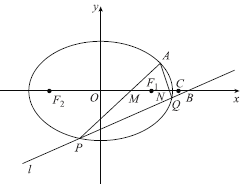
(1)求點![]() 的坐標(biāo);
的坐標(biāo);
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于點
相交于點![]() ,
,![]() ,直線
,直線![]() ,
,![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,點
兩點,點![]() ,則
,則![]() 是否為定值,如果是定值,求出這個定值,如果不是請說明理由.
是否為定值,如果是定值,求出這個定值,如果不是請說明理由.
【答案】(1)![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
試題(1)通過已知條件首先求得橢圓的標(biāo)準(zhǔn)方程,再結(jié)合三角形的面積計算公式,即可求得![]() 的坐標(biāo);(2)將直線
的坐標(biāo);(2)將直線![]() 的方程設(shè)出,聯(lián)立直線方程與橢圓方程,通過計算說明是否為定值即可.
的方程設(shè)出,聯(lián)立直線方程與橢圓方程,通過計算說明是否為定值即可.
試題解析:(1)∵橢圓![]() 過點
過點![]() ,
,![]() ,
,
∴ ,計算得
,計算得![]() ,
,![]() ,∴橢圓
,∴橢圓![]() 的方程為
的方程為![]() .
.
∵![]() 的面積
的面積![]() ,∴
,∴![]() ,∴
,∴![]() ,代入橢圓方程
,代入橢圓方程![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ;(2)法一:設(shè)直線
;(2)法一:設(shè)直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,
直線![]() 的方程為
的方程為![]() ,可得
,可得![]() ,即
,即![]() ,
,
直線![]() 的方程為
的方程為![]() ,可得
,可得![]() ,即
,即![]() .
.
聯(lián)立![]() ,消去
,消去![]() ,整理,得
,整理,得![]() .
.
由![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,
![]()
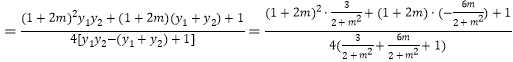
![]()
∴![]() 為定值,且
為定值,且![]() .
.
法二:設(shè)![]() ,
,![]() ,
,![]() ,
,![]() ,直線
,直線![]() ,
,![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,
![]()
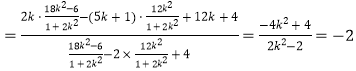 ,
,
由![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,
,
同理得![]() ,即
,即![]() ,則
,則
![]()
![]()
![]()
∴![]() 為定值,該定值為
為定值,該定值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 底面
底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點。
的中點。
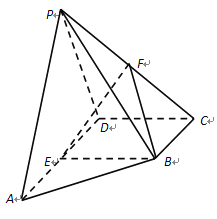
(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 在以
在以![]() 為焦點的雙曲線
為焦點的雙曲線![]() 上,過
上,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,若四邊形
,若四邊形![]() 為菱形,則該雙曲線的離心率為( )
為菱形,則該雙曲線的離心率為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為維護(hù)交通秩序,防范電動自行車被盜,天津市公安局決定,開展二輪電動自行車免費登記、上牌照工作.電動自行車牌照分免費和收費(安裝防盜裝置)兩大類,群眾可以 自愿選擇安裝.已知甲、乙、丙三個不同類型小區(qū)的人數(shù)分別為15000,15000,20000.交管部門為了解社區(qū)居民意愿,現(xiàn)采用分層抽樣的方法從中抽取10人進(jìn)行電話訪談.
(Ⅰ)應(yīng)從甲小區(qū)和丙小區(qū)的居民中分別抽取多少人?
(Ⅱ)設(shè)從甲小區(qū)抽取的居民為![]() ,丙小區(qū)抽取的居民為
,丙小區(qū)抽取的居民為![]() .現(xiàn)從甲小區(qū)和丙小區(qū)已抽取的居民中隨機(jī)抽取2人接受問卷調(diào)查.
.現(xiàn)從甲小區(qū)和丙小區(qū)已抽取的居民中隨機(jī)抽取2人接受問卷調(diào)查.
(ⅰ)試用所給字母列舉出所有可能的抽取結(jié)果;
(ⅱ)設(shè)![]() 為事件“抽取的2人來自不同的小區(qū)”,求事件
為事件“抽取的2人來自不同的小區(qū)”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() (其中
(其中![]() ),若函數(shù)
),若函數(shù)![]() 的圖象與
的圖象與![]() 軸的任意兩個相鄰交點間的距離為
軸的任意兩個相鄰交點間的距離為![]() ,且函數(shù)
,且函數(shù)![]() 的圖象過點
的圖象過點![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的單調(diào)增區(qū)間:
的單調(diào)增區(qū)間:
(3)求![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某中學(xué)甲、乙兩班共有25名學(xué)生報名參加了一項 測試.這25位學(xué)生的考分編成的莖葉圖,其中有一個數(shù)據(jù)因電腦操作員不小心刪掉了(這里暫用x來表示),但他清楚地記得兩班學(xué)生成績的中位數(shù)相同.

(Ⅰ)求這兩個班學(xué)生成績的中位數(shù)及x的值;
(Ⅱ)如果將這些成績分為“優(yōu)秀”(得分在175分 以上,包括175分)和“過關(guān)”,若學(xué)校再從這兩個班獲得“優(yōu)秀”成績的考生中選出3名代表學(xué)校參加比賽,求這3人中甲班至多有一人入選的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將高二(1)班的四個同學(xué)分到語文、數(shù)學(xué)、英語三個興趣小組,每個興趣小組至少有一名同學(xué)的分配方法有多少種?下列結(jié)論正確的有( )
A.![]() B.
B.![]()
C.![]() D.18
D.18
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經(jīng)過原點.設(shè)頂點
恰好經(jīng)過原點.設(shè)頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數(shù)
,則對函數(shù)![]() 有下列判斷:①函數(shù)
有下列判斷:①函數(shù)![]() 是偶函數(shù);②對任意的
是偶函數(shù);②對任意的![]() ,都有
,都有![]() ;③函數(shù)
;③函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;④函數(shù)
上單調(diào)遞減;④函數(shù)![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
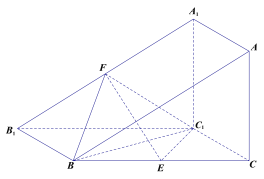
【題目】如圖,三棱柱![]() 的側(cè)面
的側(cè)面![]() 是平行四邊形,
是平行四邊形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分別是
分別是![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)當(dāng)側(cè)面![]() 是正方形,且
是正方形,且![]() 時,
時,
(ⅰ)求二面角![]() 的大小;
的大小;
(ⅱ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,指出點
?若存在,指出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com