【題目】若函數f(x)＝
為奇函數．
(1) 求a的值；
(2) 判斷f(x)的單調性．
【答案】（1）a＝－
.（2）見解析
【解析】 試題分析:（1）由奇函數定義得f(－x)＋f(x)＝0，利用負分數指數冪化簡解得a＝－
.（2）先求函數定義域，將函數分離得
，再利用復合函數單調性研究函數在(0，＋∞)上單調性，結合奇函數性質得函數在(－∞，0)上單調性
試題解析：解：(1) ∵ f(x)＝
＝a－
.
由f(－x)＋f(x)＝0，
得a－
＋a－＝0，
∴ 2a＋
＝0，
∴ a＝－
.
(2) ∵ f(x)＝－－，
∴ 2x－1≠0，即x≠0，
∴ 函數f(x)＝－－的定義域為{x|x≠0}．
設x2>x1>0，則2x2>2x1>1，2x2－1>2x1－1>0，
＜
，－＞－，－－＞－－，
∴ f(x2)＞f(x1)，
∴ 函數f(x)在(0，＋∞)上是增函數，同理f(x)在(－∞，0)上也是增函數．
備戰中考寒假系列答案科目：高中數學 來源： 題型：
【題目】某校高一（1）班有男同學45名，女同學15名，老師按照分層抽樣的方法抽取4人組建了一個課外興趣小組.
（I）求課外興趣小組中男、女同學的人數；
（II）經過一個月的學習、討論，這個興趣小組決定選出兩名同學做某項實驗，方法是從小組里選出一名同學做實驗，該同學做完后，再從小組內剩下的同學中選出一名同學做實驗，求選出的兩名同學中恰有一名女同學的概率；
（III）在（II）的條件下，第一次做實驗的同學A得到的實驗數據為38,40,41,42,44，第二次做實驗的同學B得到的實驗數據為39,40,40,42,44，請問哪位同學的實驗更穩定？并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f(x)滿足f(x＋1)－f(x)＝－2x＋1，且f(2)＝15.
(1)求函數f(x)的解析式；
(2) 令g(x)＝(2－2m)x－f(x)．
① 若函數g(x)在x∈[0，2]上是單調函數，求實數m的取值范圍；
② 求函數g(x)在x∈[0，2]上的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，短軸兩個端點為
，且四邊形
是邊長為2的正方形．
（1）求橢圓的方程；
（2）若
分別是橢圓長軸的左、右端點，動點
滿足
，連結
，交橢圓于點
，證明：
為定值；
（3）在（2）的條件下，試問
軸上是否存在異于點
的定點
，使得以
為直徑的圓恒過直線
的交點，若存在，求出點
的坐標；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，短軸一個端點到右焦點的距離為
.
（1） 求橢圓
的方程;
（2） 設直線
與橢圓交于
、
兩點，坐標原點
到直線
的距離為
，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量a＝(cos α，sin α)，b＝(cos β，sin β)，c＝(－1，0)．
(1) 求向量b＋c的模的最大值；
(2) 若α＝
，且a⊥(b＋c)，求cos β的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝loga(ax2－x＋1)(a＞0，a≠1)．
(1) 若a＝
，求函數f(x)的值域．
(2) 當f(x)在區間
上為增函數時，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數（Air Quality Index，簡稱
）是定量描述空氣質量狀況的指數，空氣質量按照大小分為六級，
為優；
為輕度污染；
為中度污染；
為重度污染；
為嚴重污染．一環保人士記錄去年某地某月10天的的莖葉圖如右．
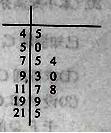
（1）利用該樣本估計該地本月空氣質量優良（
）的天數；（按這個月總共30天計算）
（2）將頻率視為概率，從本月中隨機抽取3天，記空氣質量優良的天數為
，求
的概率分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
