
【題目】已知拋物線![]() ,且拋物線
,且拋物線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() ,直線
,直線![]() 與拋物線交于
與拋物線交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側(cè)),且直線
左側(cè)),且直線![]() 垂直于直線
垂直于直線![]() .
.
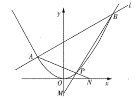
(1)求證:直線![]() 過定點,并求出定點坐標(biāo);
過定點,并求出定點坐標(biāo);
(2)如圖,直線![]() 交
交![]() 軸于點
軸于點![]() ,直線
,直線![]() 交
交![]() 軸于點,求
軸于點,求![]() 的最大值.
的最大值.
【答案】(1)證明見解析,定點![]() ;(2)50
;(2)50
【解析】
(1)首先根據(jù)題意求出拋物線方程,然后求出點![]() 的坐標(biāo),再由直線
的坐標(biāo),再由直線![]() 互相垂直,求出直線
互相垂直,求出直線![]() 的斜率,求出直線
的斜率,求出直線![]() 的方程,進而可得定點坐標(biāo);
的方程,進而可得定點坐標(biāo);
(2)首先設(shè)出直線![]() 的方程,然后聯(lián)立直線與拋物線的方程,求出
的方程,然后聯(lián)立直線與拋物線的方程,求出![]() 的橫坐標(biāo),最后利用弦長公式,即可求解.
的橫坐標(biāo),最后利用弦長公式,即可求解.
(1)由題意可得![]() .
.
當(dāng)![]() 時,
時,![]() ,
,
![]()
![]() 拋物線
拋物線![]() 的方程為
的方程為![]() .
.
![]() .
.
設(shè)![]() ,
,
![]() ,
,
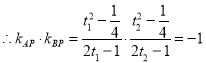 ,
,
化簡得![]() .
.![]()
![]()
又![]()
![]() ,
,
![]() 直線
直線![]() 的方程為
的方程為![]() ,
,
即![]() .
.
將![]() 式代入直線
式代入直線![]() 的方程,得:
的方程,得:![]() ,
,
令![]() ,則
,則![]() ,
,
可得直線![]() 過定點
過定點![]() .
.
(2)設(shè)直線![]() 的方程為
的方程為![]() ,
,
不妨設(shè)![]() ,易知
,易知![]() ,
,
聯(lián)立,得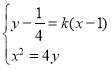 ,得
,得![]() ,
,
![]() ,
,
利用根與系數(shù)的關(guān)系得![]()
![]()
![]()
![]() 同理可得
同理可得![]() ,
,
易知![]() ,
,
![]()
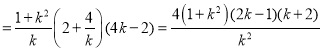
![]() ,
,
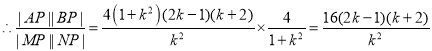
![]() ,
,
![]() 的最大值為50.
的最大值為50.


科目:高中數(shù)學(xué) 來源: 題型:
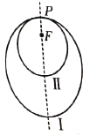
【題目】嫦娥四號任務(wù)經(jīng)過探月工程重大專項領(lǐng)導(dǎo)小組審議,通過并且正式開始實施,如圖所示.假設(shè)“嫦娥四號”衛(wèi)星將沿地月轉(zhuǎn)移軌道飛向月球后,在月球附近一點![]() 變軌進入以月球球心
變軌進入以月球球心![]() 為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛(wèi)星在
為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛(wèi)星在![]() 點第二次變軌進入仍以
點第二次變軌進入仍以![]() 為一個焦點的橢圓軌道Ⅱ繞月飛行.若用
為一個焦點的橢圓軌道Ⅱ繞月飛行.若用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用
分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的長軸長,則下列關(guān)系中正確的是( )
分別表示橢圓軌道Ⅰ和Ⅱ的長軸長,則下列關(guān)系中正確的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E: ![]() 經(jīng)過點P(2,1),且離心率為
經(jīng)過點P(2,1),且離心率為![]() .
.
(Ⅰ)求橢圓的標(biāo)準方程;
(Ⅱ)設(shè)O為坐標(biāo)原點,在橢圓短軸上有兩點M,N滿足![]() ,直線PM、PN分別交橢圓于A,B.探求直線AB是否過定點,如果經(jīng)過定點請求出定點的坐標(biāo),如果不經(jīng)過定點,請說明理由.
,直線PM、PN分別交橢圓于A,B.探求直線AB是否過定點,如果經(jīng)過定點請求出定點的坐標(biāo),如果不經(jīng)過定點,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2019年10月20日,第六屆世界互聯(lián)網(wǎng)大會發(fā)布了15項“世界互聯(lián)網(wǎng)領(lǐng)先科技成果”,其中有5項成果均屬于芯片領(lǐng)域,分別為華為高性能服務(wù)器芯片“鯤鵬920”、清華大學(xué)“面向通用人工智能的異構(gòu)融合天機芯片”、“特斯拉全自動駕駛芯片”、寒武紀云端AI芯片、“思元270”、賽靈思“Versal自適應(yīng)計算加速平臺”.現(xiàn)有3名學(xué)生從這15項“世界互聯(lián)網(wǎng)領(lǐng)先科技成果”中分別任選1項進行了解,且學(xué)生之間的選擇互不影響,則至少有1名學(xué)生選擇“芯片領(lǐng)域”的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某果園今年的臍橙豐收了,果園準備利用互聯(lián)網(wǎng)銷售.為了更好的銷售,現(xiàn)隨機摘下了![]() 個臍橙進行測重,其質(zhì)量分布在區(qū)間
個臍橙進行測重,其質(zhì)量分布在區(qū)間![]() 內(nèi)(單位:克),統(tǒng)計質(zhì)量的數(shù)據(jù)作出頻率分布直方圖如下圖所示:
內(nèi)(單位:克),統(tǒng)計質(zhì)量的數(shù)據(jù)作出頻率分布直方圖如下圖所示:
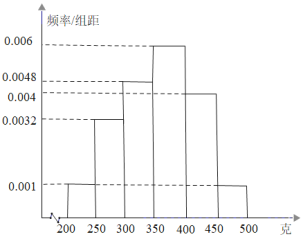
(1)按分層抽樣的方法從質(zhì)量落在![]() ,
,![]() 的臍橙中隨機抽取
的臍橙中隨機抽取![]() 個,再從這
個,再從這![]() 個臍橙中隨機抽
個臍橙中隨機抽![]() 個,求這
個,求這![]() 個臍橙質(zhì)量都不小于
個臍橙質(zhì)量都不小于![]() 克的概率;
克的概率;
(2)以各組數(shù)據(jù)的中間數(shù)值代表這組數(shù)據(jù)的平均水平,以頻率代表概率,已知該果園的臍橙樹上大約還有![]() 個臍橙待出售,某電商提出兩種收購方案:甲:所有臍橙均以
個臍橙待出售,某電商提出兩種收購方案:甲:所有臍橙均以![]() 元/千克收購;乙:低于
元/千克收購;乙:低于![]() 克的臍橙以
克的臍橙以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.請通過計算為該果園選擇收益最好的方案.
元/個收購.請通過計算為該果園選擇收益最好的方案.
(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l的參數(shù)方程為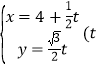 為參數(shù)
為參數(shù)![]() ,以坐標(biāo)原點為極點,x軸的正半軸為極軸建建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為
,以坐標(biāo)原點為極點,x軸的正半軸為極軸建建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]() .
.
![]() 求曲線C的直角坐標(biāo)方程與直線l的極坐標(biāo)方程;
求曲線C的直角坐標(biāo)方程與直線l的極坐標(biāo)方程;
![]() Ⅱ
Ⅱ![]() 若直線
若直線![]() 與曲線C交于點
與曲線C交于點![]() 不同于原點
不同于原點![]() ,與直線l交于點B,求
,與直線l交于點B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的奇數(shù)項是公差為
的奇數(shù)項是公差為![]() 的等差數(shù)列,偶數(shù)項是公差為
的等差數(shù)列,偶數(shù)項是公差為![]() 的等差數(shù)列,
的等差數(shù)列, ![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項和,
項和, ![]()
(1)若![]() ,求
,求![]() ;
;
(2)已知![]() ,且對任意的
,且對任意的![]() ,有
,有![]() 恒成立,求證:數(shù)列
恒成立,求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(3)若![]() ,且存在正整數(shù)
,且存在正整數(shù)![]() ,使得
,使得![]() ,求當(dāng)
,求當(dāng)![]() 最大時,數(shù)列
最大時,數(shù)列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知圓柱內(nèi)有一個三棱錐![]() ,
,![]() 為圓柱的一條母線,
為圓柱的一條母線,![]() ,
,![]() 為下底面圓
為下底面圓![]() 的直徑,
的直徑,![]() ,
,![]() .
.

(1)在圓柱的上底面圓內(nèi)是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?證明你的結(jié)論.
?證明你的結(jié)論.
(2)設(shè)點![]() 為棱
為棱![]() 的中點,
的中點,![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,AD=AP=3,點M是棱PD的中點.
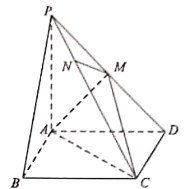
(1)求二面角M—AC—D的余弦值;
(2)點N是棱PC上的點,已知直線MN與平面ABCD所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com