Question

【題目】已知函數f（x）=ln（x+1）+ax，其中a∈R．
（Ⅰ） 當a=﹣1時，求證：f（x）≤0；
（Ⅱ） 對任意x2≥ex1＞0，存在x∈（﹣1，+∞），使 成立，求a的取值范圍．（其中e是自然對數的底數，e=2.71828…）

Answer 1

【答案】解：（Ⅰ）證明：當 a=﹣1時，f（x）=ln（x+1）﹣x（x＞﹣1），
則 ，令f'（x）=0，得x=0．
當﹣1＜x＜0時，f'（x）＞0，f（x）單調遞增；
當x＞0時，f'（x）＜0，f（x）單調遞減．
故當x=0時，函數f（x）取得極大值，也為最大值，
所以f（x）max=f（0）=0，
所以，f（x）≤0，得證．
（Ⅱ）不等式 ，
即為 ．
而
= ．
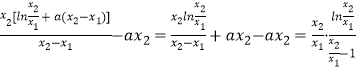令 ．故對任意t≥e，存在x∈（﹣1，+∞），使 恒成立，
所以 ，
設 ，則 ，
設u（t）=t﹣1﹣lnt，知 對于t≥e恒成立，
則u（t）=t﹣1﹣lnt為[e，+∞）上的增函數，
于是u（t）=t﹣1﹣lnt≥u（e）=e﹣2＞0，
即 對于t≥e恒成立，
所以 為[e，+∞）上的增函數，
所以 ；
設p（x）=﹣f（x）﹣a，即p（x）=﹣ln（x+1）﹣ax﹣a，
當a≥0時，p（x）為（0，+∞）上的減函數，
且其值域為R，可知符合題意．
當a＜0時， ，由p'（x）=0可得 ，
由p'（x）＞0得 ，則p（x）在 上為增函數，
由p'（x）＜0得 ，則p（x）在 上為減函數，
所以 ．
從而由 ，解得 ，
綜上所述，a的取值范圍是
【解析】（Ⅰ）求出函數的導數，通過討論a的范圍，求出函數的單調區間，從而證明結論即可；（Ⅱ）令 ，問題轉化為 ，設 ，根據函數的單調性證明即可．
【考點精析】關于本題考查的利用導數研究函數的單調性，需要了解一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減才能得出正確答案．