Question

【題目】在高中學習過程中，同學們經常這樣說“如果物理成績好，那么學習數學就沒什么問題”某班針對“高中生物理對數學學習的影響”進行研究，得到了學生的物理成績與數學成績具有線性相關關系的結論，現從該班隨機抽取5名學生在一次考試中的物理和數學成績，如表：

編號成績	1	2	3	4	5
物理(x)	90	85	74	68	63
數學(y)	130	125	110	95	90

(1)求數學y成績關于物理成績x的線性回歸方程(精確到0.1)，若某位學生的物理成績為80分時，預測他的數學成績．

(2)要從抽取的這五位學生中隨機選出三位參加一項知識競賽，以x表示選中的學生的數學成績高于100分的人數，求隨機變量X的分布列及數學期望．

Answer 1

【答案】(1) , 預測他的數學成績是116

(2) X的分布列為：

X	1	2	3
p

E（X）＝1.8．

【解析】

（1）根據表中數據計算、 ，求出回歸系數 、 ，寫出回歸方程，

利用回歸方程計算x＝80時 的值即可；

（2）抽取的五位學生中成績高于100分的有3人，X的可以取1，2，3，

計算對應的概率值，寫出X的分布列，計算數學期望值．

解：（1）根據表中數據計算＝ ×（90+85+74+68+63）＝76，

＝×（130+125+110+95+90）＝110，

＝902+852+742+682+632＝29394，

＝90×130+85×125+74×110+68×95+63×90＝42595，

＝/span> ＝ ，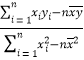

；

∴x、y的線性回歸方程是，

當x＝80時， ＝1.5×80﹣4＝116，

即某位同學的物理成績為80分，預測他的數學成績是116；

（2）抽取的五位學生中成績高于100分的有3人，

X表示選中的同學中高于100分的人數，可以取1，2，3，

P（X＝1）＝，P（X＝2）＝，

P（X＝3）＝；

故X的分布列為：

X	1	2	3
p

X的數學期望值為E（X）＝1× +2×+3× ＝1.8．