
���}Ŀ����D��ij��������![]() ��
��![]() ��
��![]() ����(g��)С�u����e��С���Բ�Ӌ(j��)����
����(g��)С�u����e��С���Բ�Ӌ(j��)����![]() �u��
�u��![]() �u�ı�ƫ�|
�u�ı�ƫ�|![]() �����
�����![]() �u
�u![]() ǧ��̎��
ǧ��̎��![]() �u��
�u��![]() �u�����|�����
�u�����|�����![]() �u20ǧ��̎.��
�u20ǧ��̎.��![]() ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)��![]() �����|����?y��n)?/span>
�����|����?y��n)?/span>![]() �S��������1ǧ�מ��λ�L(zh��ng)�ȣ�����ƽ��ֱ������(bi��o)ϵ.�A
�S��������1ǧ�מ��λ�L(zh��ng)�ȣ�����ƽ��ֱ������(bi��o)ϵ.�A![]() ��(j��ng)�^
��(j��ng)�^![]() ��
��![]() ��
��![]() ���c(di��n).
���c(di��n).

��1����A![]() �ķ��̣�
�ķ��̣�
��2����A![]() �^(q��)���(n��i)��δ֪�������F(xi��n)��һ��D��
�^(q��)���(n��i)��δ֪�������F(xi��n)��һ��D��![]() �u����ƫ��30�������
�u����ƫ��30�������![]() �u40ǧ��̎����������ƫ�|
�u40ǧ��̎����������ƫ�|![]() ��������׃����ԇ��ԓ���Л]���|����Σ�U(xi��n)��
��������׃����ԇ��ԓ���Л]���|����Σ�U(xi��n)��
���𰸡���1��![]() ��2��ԓ�����|����Σ�U(xi��n)
��2��ԓ�����|����Σ�U(xi��n)
��������
��1���ɈA�^�c(di��n)![]() ��
��![]() ��
��![]() ���O(sh��)�A
���O(sh��)�A![]() �ķ��̞�
�ķ��̞�![]() ��
��
�ٌ��c(di��n)![]() ��
��![]() ��
��![]() ������(bi��o)�����\(y��n)�㼴�ɵý⣻
������(bi��o)�����\(y��n)�㼴�ɵý⣻
��2�����}��ɵ�ԓ�����з���?y��n)�ֱ��![]() ��
��![]() ���ٽY(ji��)���c(di��n)��ֱ���ľ��x��ʽ�ɵÈA��
���ٽY(ji��)���c(di��n)��ֱ���ľ��x��ʽ�ɵÈA��![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ���ý�.
���ý�.
�⣺��1����D��ʾ��![]() ��
��![]() ��
��
�O(sh��)�^![]() ��
��![]() ��
��![]() ���c(di��n)�ĈA
���c(di��n)�ĈA![]() �ķ��̞�
�ķ��̞�![]() ��
��
�ã�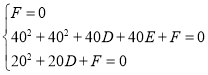 ��
��
���![]() ��
��![]() ��
��![]() ��
��
�����ԈA![]() �ķ��̞�
�ķ��̞�![]() ��
��
�A�Ğ�![]() ���돽
���돽![]() ��
��
��2��ԓ����ʼλ�Þ��c(di��n)![]() ���t
���t![]() ��
��
��ԓ����������ֱ��![]() ��б�ʞ�1��
��б�ʞ�1��
��ԓ�����з���?y��n)�ֱ��![]() ��
��![]() ��
��
���ڈA��![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
��ԓ�����|����Σ�U(xi��n).


 �n��С���I(y��)ϵ�д�
�n��С���I(y��)ϵ�д� �S��С��Ԫ�������㾚��(x��)��(c��)ϵ�д�
�S��С��Ԫ�������㾚��(x��)��(c��)ϵ�д� �ɹ�Ӗ(x��n)��Ӌ(j��)��ϵ�д�
�ɹ�Ӗ(x��n)��Ӌ(j��)��ϵ�д� ����Ӗ(x��n)����ֱͨ�п����c(di��n)ϵ�д�
����Ӗ(x��n)����ֱͨ�п����c(di��n)ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У���I(y��)��ϵ�д�
��У���I(y��)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
��1����![]() �����C��
�����C��![]()
��2����![]() ������
������![]() ����(sh��)��(sh��)
����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ľ��x�c
�ľ��x�c![]() ����ֱ��
����ֱ��![]() �ľ��x�ıȞ�
�ľ��x�ıȞ�![]() ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() ��܉�Eӛ��
��܉�Eӛ��![]() .
.
��1����܉�E![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n)![]() ��܉�E
��܉�E![]() ���\(y��n)��(d��ng)���c(di��n)
���\(y��n)��(d��ng)���c(di��n)![]() �ڈA
�ڈA![]() ���\(y��n)��(d��ng)���ҿ���
���\(y��n)��(d��ng)���ҿ���![]() ��
��
��![]() ��ȡֵ������
��ȡֵ������
��3���^�c(di��n)![]() �Ą�(d��ng)ֱ��
�Ą�(d��ng)ֱ��![]() ��܉�E
��܉�E![]() ��
��![]() ���c(di��n)��ԇ��:�ڴ�����(bi��o)ƽ�����Ƿ����һ��(g��)���c(di��n)
���c(di��n)��ԇ��:�ڴ�����(bi��o)ƽ�����Ƿ����һ��(g��)���c(di��n)![]() ��ʹ�ßo(w��)Փ
��ʹ�ßo(w��)Փ![]() ����D(zhu��n)��(d��ng)����
����D(zhu��n)��(d��ng)����![]() ��ֱ���ĈA���^�c(di��n)
��ֱ���ĈA���^�c(di��n)![]() ?�����ڣ�����c(di��n)
?�����ڣ�����c(di��n)![]() ������(bi��o).�������ڣ�Ո(q��ng)�f������.
������(bi��o).�������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�����̈�(ch��ng)ȥ���(gu��)�c���g��Ӌ(j��)����![]() �f(w��n)��ُ(g��u)��Σ������S�C(j��)���
�f(w��n)��ُ(g��u)��Σ������S�C(j��)���![]() ������(du��)ÿ�����M(f��i)���~�M(j��n)�нy(t��ng)Ӌ(j��)�õ��±���
������(du��)ÿ�����M(f��i)���~�M(j��n)�нy(t��ng)Ӌ(j��)�õ��±���
���M(f��i)���~����λ��Ԫ�� |
|
|
|
|
|
ُ(g��u)��Ώ���(sh��) | 25 | 25 | 30 | 10 | 10 |
���ڹ����ˆTʧ�`����əڔ�(sh��)��(j��)�џo(w��)�����R(sh��)������(d��ng)�r(sh��)ӛ䛱���������(j��)�����ϔ�(sh��)��(j��)�L�Ƴɵ��l�ʷֲ�ֱ���D����Ӌ(j��)����ÿ�����M(f��i)�~����λ��(sh��)�cƽ����(sh��)ǡ�����.���l�ʹ�Ӌ(j��)���ʣ�������І��}��
��1����Ӌ(j��)ȥ���(gu��)�c���gԓ�̈�(ch��ng)��Ӌ(j��)���ɵ�ُ(g��u)����У��ιP���M(f��i)�~���^![]() Ԫ�ĸ��ʣ�
Ԫ�ĸ��ʣ�
��2����Ą�(l��)����M(f��i)��ԓ�̈�(ch��ng)�����ڽ����(gu��)�c���g�M(j��n)�д��N���(d��ng)�����ιP���M(f��i)���^![]() Ԫ�ߣ��ɳ骄(ji��ng)һ�Σ���һ�Ȫ�(ji��ng)�����Ȫ�(ji��ng)�����Ȫ�(ji��ng)��Ϳ��Էքe�@�Ãr(ji��)ֵ
Ԫ�ߣ��ɳ骄(ji��ng)һ�Σ���һ�Ȫ�(ji��ng)�����Ȫ�(ji��ng)�����Ȫ�(ji��ng)��Ϳ��Էքe�@�Ãr(ji��)ֵ![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��![]() Ԫ�Ī�(ji��ng)Ʒ.��֪�Ъ�(ji��ng)�ʞ�
Ԫ�Ī�(ji��ng)Ʒ.��֪�Ъ�(ji��ng)�ʞ�![]() ����һ�Ȫ�(ji��ng)�����Ȫ�(ji��ng)�����Ȫ�(ji��ng)���Ъ�(ji��ng)�����Θ�(g��u)�ɵȱȔ�(sh��)�У�����һ�Ȫ�(ji��ng)���Ъ�(ji��ng)�ʞ�
����һ�Ȫ�(ji��ng)�����Ȫ�(ji��ng)�����Ȫ�(ji��ng)���Ъ�(ji��ng)�����Θ�(g��u)�ɵȱȔ�(sh��)�У�����һ�Ȫ�(ji��ng)���Ъ�(ji��ng)�ʞ�![]() .�������(gu��)�c���gԓ�̈�(ch��ng)��ُ(g��u)��Δ�(sh��)����ȥ��ͬ�����L(zh��ng)
.�������(gu��)�c���gԓ�̈�(ch��ng)��ُ(g��u)��Δ�(sh��)����ȥ��ͬ�����L(zh��ng)![]() ��ʽ�A(y��)�y(c��)�̈�(ch��ng)�����(gu��)�c���g���k��(ji��ng)Ʒ���_�N.
��ʽ�A(y��)�y(c��)�̈�(ch��ng)�����(gu��)�c���g���k��(ji��ng)Ʒ���_�N.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У���ԭ�c(di��n)
�У���ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ.��֪����
�S�ķ�ؓ(f��)���S��O�S�����O����(bi��o)ϵ.��֪����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��![]() ������
������![]() �ϵĄ�(d��ng)�c(di��n)��
�ϵĄ�(d��ng)�c(di��n)��![]() �c
�c![]() �S��
�S��![]() �S�������S�քe����
�S�������S�քe����![]() ��
��![]() ���c(di��n).
���c(di��n).
��1����![]() ���c(di��n)
���c(di��n)![]() ��܉�E�ą���(sh��)���̣�
��܉�E�ą���(sh��)���̣�
��2����![]() �ǣ�1�����c(di��n)
�ǣ�1�����c(di��n)![]() ��܉�E�ϵĄ�(d��ng)�c(di��n)����
��܉�E�ϵĄ�(d��ng)�c(di��n)����![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���P(gu��n)�ڈA���ʣ���(sh��)�W(xu��)�l(f��)չʷ�ϳ��F(xi��n)�^����Є�(chu��ng)����������������Sԇ�(y��n)�����䆢�l(f��)���҂�Ҳ����ͨ�^�O(sh��)Ӌ(j��)�����ԇ�(y��n)����Ӌ(j��)![]() ��ֵ��ԇ�(y��n)���E���£�����Ո(q��ng)�߶��꼉(j��)
��ֵ��ԇ�(y��n)���E���£�����Ո(q��ng)�߶��꼉(j��)![]() ��ͬ�W(xu��)ÿ����С��Ƭ���S�C(j��)����һ��(g��)��(sh��)��(sh��)��(du��)
��ͬ�W(xu��)ÿ����С��Ƭ���S�C(j��)����һ��(g��)��(sh��)��(sh��)��(du��)![]() ��������Ƭ�ϵ�
��������Ƭ�ϵ�![]() ��
��![]() ���c
���c![]() ��(g��u)���J�������Σ��t���˿�Ƭ�Ͻ����۽y(t��ng)Ӌ(j��)�Ͻ��Ŀ�Ƭ��(sh��)��ӛ��
��(g��u)���J�������Σ��t���˿�Ƭ�Ͻ����۽y(t��ng)Ӌ(j��)�Ͻ��Ŀ�Ƭ��(sh��)��ӛ��![]() ���ܸ���(j��)�y(t��ng)Ӌ(j��)��(sh��)
���ܸ���(j��)�y(t��ng)Ӌ(j��)��(sh��)![]() ��
��![]() ��Ӌ(j��)
��Ӌ(j��)![]() ��ֵ.��ô���Թ�Ӌ(j��)
��ֵ.��ô���Թ�Ӌ(j��)![]() ��ֵ�s�飨 ��
��ֵ�s�飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij������˾���˷���������У��ƌW(xu��)Ҏ(gu��)��܇�vͶ�ţ���һ��(g��)�ˆT�ܼ�����(d��ng)�ض����O(sh��)һ��(g��)���c(di��n)վ�������о�܇�v�l(f��)܇�g���r(sh��)�gx�c�˿͵Ⱥ��˔�(sh��)y֮�g���P(gu��n)ϵ����(j��ng)�^�{(di��o)��õ�����(sh��)��(j��)��
�g���r(sh��)�gx/�� | 10 | 11 | 12 | 13 | 14 | 15 |
�Ⱥ��˔�(sh��)y/�� | 23 | 25 | 26 | 29 | 28 | 31 |
�{(di��o)��С�M�ȏ��@6�M��(sh��)��(j��)���xȡ4�M��(sh��)��(j��)���Իؚw���̣�����ʣ�µ�2�M��(sh��)��(j��)�M(j��n)�Йz�(y��n).�z�(y��n)�������£�������õľ��Իؚw����Ӌ(j��)���g���r(sh��)�g��(du��)��(y��ng)�ĵȺ��˔�(sh��)![]() ������
������![]() �c��(sh��)�H�Ⱥ��˔�(sh��)y�IJ����ֵ�Ľ^��(du��)ֵ�������^1���t�Q�����ǡ�ǡ��(d��ng)�ؚw���̡�.
�c��(sh��)�H�Ⱥ��˔�(sh��)y�IJ����ֵ�Ľ^��(du��)ֵ�������^1���t�Q�����ǡ�ǡ��(d��ng)�ؚw���̡�.
��1�����@6�M��(sh��)��(j��)���S�C(j��)�xȡ4�M��(sh��)��(j��)����ʣ�µ�2�M��(sh��)��(j��)���g���r(sh��)�g�����ĸ��ʣ�
��2�����xȡ�������g4�M��(sh��)��(j��)����y�P(gu��n)��x�ľ��Իؚw����![]() �����Д�˷����Ƿ��ǡ�ǡ��(d��ng)�ؚw���̡�.
�����Д�˷����Ƿ��ǡ�ǡ��(d��ng)�ؚw���̡�.
������(du��)��һ�M��(sh��)��(j��)![]() ����ؚwֱ��
����ؚwֱ��![]() ��б�ʺͽؾ����С���˹�Ӌ(j��)�քe�飺
��б�ʺͽؾ����С���˹�Ӌ(j��)�քe�飺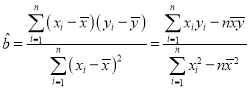 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���E�A![]() ��
�� ![]() ���x���ʞ�
���x���ʞ�![]() �����S���c(di��n)�c�ɽ��c(di��n)���ɵ���������e��
�����S���c(di��n)�c�ɽ��c(di��n)���ɵ���������e��![]() .
.
(1)��E�A![]() �ķ��̣�
�ķ��̣�
(2)�O(sh��)ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)�����^�c(di��n)
���c(di��n)�����^�c(di��n)![]() ��
��![]() ������(bi��o)ԭ�c(di��n)����(d��ng)��
������(bi��o)ԭ�c(di��n)����(d��ng)��![]() ��ֱ�������Σ���ֱ��
��ֱ�������Σ���ֱ��![]() ��б��.
���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)��c(di��n)![]() �M��
�M��![]() ��ӛM��܉�E������C��ֱ��l��
��ӛM��܉�E������C��ֱ��l��![]() ��
��![]() ��������C��P��Q���c(di��n)���c(di��n)P�ڵ�һ���ޣ�
��������C��P��Q���c(di��n)���c(di��n)P�ڵ�һ���ޣ�![]() �S�������E���B��QE�����L(zh��ng)������C���c(di��n)G.
�S�������E���B��QE�����L(zh��ng)������C���c(di��n)G.
��1��������C�ķ��̣����f������C��ʲô������
��2����![]() ����
����![]() ����e.
����e.
��3����![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com