
【題目】某高校為增加應屆畢業生就業機會,每年根據應屆畢業生的綜合素質和學業成績對學生進行綜合評估,已知某年度參與評估的畢業生共有2000名,其評估成績![]() 近似的服從正態分布
近似的服從正態分布![]() .現隨機抽取了100名畢業生的評估成績作為樣本,并把樣本數據進行了分組,繪制了頻率分布直方圖:
.現隨機抽取了100名畢業生的評估成績作為樣本,并把樣本數據進行了分組,繪制了頻率分布直方圖:
(1)求樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(2)若學校規定評估成績超過![]() 分的畢業生可參加
分的畢業生可參加![]() 三家公司的面試.
三家公司的面試.
(ⅰ)用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() ,請利用估計值判斷這2000名畢業生中,能夠參加三家公司面試的人數;
,請利用估計值判斷這2000名畢業生中,能夠參加三家公司面試的人數;
(ⅱ)若三家公司每家都提供甲、乙、丙三個崗位,崗位工資表如下:
公司 | 甲崗位 | 乙崗位 | 丙崗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李華同學取得了三個公司的面試機會,經過評估,李華在三個公司甲、乙、丙三個崗位的面試成功的概率均為![]() ,李華準備依次從
,李華準備依次從![]() 三家公司進行面試選崗,公司規定:面試成功必須當場選崗,且只有一次機會.李華在某公司選崗時,若以該崗位工資與未進行面試公司的工資期望作為抉擇依據,問李華可以選擇
三家公司進行面試選崗,公司規定:面試成功必須當場選崗,且只有一次機會.李華在某公司選崗時,若以該崗位工資與未進行面試公司的工資期望作為抉擇依據,問李華可以選擇![]() 公司的哪些崗位?
公司的哪些崗位?
并說明理由.
附:![]() ,若隨機變量
,若隨機變量![]() ,
,
則![]() .
.
【答案】(1)70,161;(2)(ⅰ)317人;(ⅱ)李華可以選擇![]() 公司的甲崗位,
公司的甲崗位,![]() 公司的甲、乙崗位,
公司的甲、乙崗位,![]() 公司的三個崗位.
公司的三個崗位.
【解析】
(1)由樣本平均數定義直接計算即可得到平均數,由樣本方差公式直接計算即可得到樣本方差,問題得解。
(2)(ⅰ)利用正態分布的對稱性直接求解。
(ⅱ)利用表中數據求得B公司的工資期望為7260(元),C公司的工資期望為6800(元),由表中數據即可抉擇。
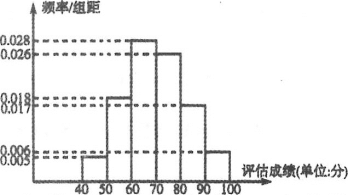
(1)由所得數據繪制的頻率直方圖,得:
樣本平均數![]() =45×0.05+55×0.18+65×0.28+75×0.26+85×0.17+95×0.06=70;
=45×0.05+55×0.18+65×0.28+75×0.26+85×0.17+95×0.06=70;
樣本方差s2=(45-70)2×0.05+(55-70)2×0.18+(65-70)2×0.28+(75-70)2×0.26+(85-70)2×0.17+(95-70)2×0.06=161;
(2)(i)由(1)可知,![]() ,
,![]() ,故評估成績Z服從正態分布N(70,161),
,故評估成績Z服從正態分布N(70,161),
所以![]() .
.
在這2000名畢業生中,能參加三家公司面試的估計有2000×0.1587≈317人.
(ii)李華可以選擇A公司的甲崗位,B公司的甲、乙崗位,C公司的三個崗位.
理由如下:
設B、C公司提供的工資為XB,XC,則XB,XC都為隨機變量,其分布列為
公司 | 甲崗位 | 乙崗位 | 丙崗位 |
XB | 9800 | 7200 | 5400 |
XC | 10000 | 6000 | 5000 |
P | 0.3 | 0.3 | 0.4 |
則B公司的工資期望:E(XB)=9800×0.3+7200×0.3+5400×0.4=7260(元),
C公司的工資期望:E(XC)=10000×0.3+6000×0.3+5000×0.4=6800(元),
因為A公司的甲崗位工資9600元大于B、C公司的工資期望,乙崗位工資6400元小于B、C公司的工資期望,故李華先去A公司面試,若A公司給予甲崗位就接受,否則去B公司;B公司甲、乙崗位工資都高于C公司的工資期望,故B公司提供甲、乙崗位就接受,否則去C公司;在C公司可以依次接受甲、乙、丙三種崗位中的一種崗位.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
【題目】已知球的半徑為4,球面被互相垂直的兩個平面所截,得到的兩個圓的公共弦長為2![]() .若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
.若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲、乙、丙三名學生參加某大學的自主招生考試,考試分兩輪,第一輪筆試,第二輪面試,只有第一輪筆試通過才有資格進入第二輪面試,面試通過就可以在高考錄取中獲得該校的優惠加分,兩輪考試相互獨立.根據以往多次的模擬測試,甲、乙、丙三名學生能通過筆試的概率分別為0.4,0.8,0.5,能通過面試的概率分別為0.8,0.4,0.64.根據這些數據我們可以預測:
(1)甲、乙、丙三名學生中至少有兩名學生通過第一輪筆試的概率;
(2)甲、乙、丙三名學生能獲得該校優惠加分的人數![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
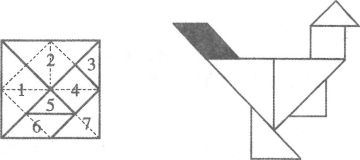
【題目】七巧板是一種古老的中國傳統智力玩具,是由七塊板組成的.而這七塊板可拼成許多圖形,例如:三角形、不規則多邊形、各種人物、動物、建筑物等,清陸以湉《冷廬雜識》寫道:近又有七巧圖,其式五,其數七,其變化之式多至千余.在18世紀,七巧板流傳到了國外,至今英國劍橋大學的圖書館里還珍藏著一部《七巧新譜》.若用七巧板拼成一只雄雞,在雄雞平面圖形上隨機取一點,則恰好取自雄雞雞尾(陰影部分)的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 的底面為直角梯形,
的底面為直角梯形,![]() ,
,![]() °,
°,![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)求![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)求平面![]() 與平面
與平面![]() 所成二面角(銳角)的余弦值.
所成二面角(銳角)的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自貢農科所實地考察,研究發現某貧困村適合種植![]() ,
,![]() 兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統計數據:藥材
兩種藥材,可以通過種植這兩種藥材脫貧.通過大量考察研究得到如下統計數據:藥材![]() 的畝產量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
的畝產量約為300公斤,其收購價格處于上漲趨勢,最近五年的價格如下表:
編號 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
單價(元/公斤) | 18 | 20 | 23 | 25 | 29 |
藥材![]() 的收購價格始終為20元/公斤,其畝產量的頻率分布直方圖如下:
的收購價格始終為20元/公斤,其畝產量的頻率分布直方圖如下:

(1)若藥材![]() 的單價
的單價![]() (單位:元/公斤)與年份編號
(單位:元/公斤)與年份編號![]() 具有線性相關關系,請求出
具有線性相關關系,請求出![]() 關于
關于![]() 的回歸直線方程,并估計2020年藥材
的回歸直線方程,并估計2020年藥材![]() 的單價;
的單價;
(2)用上述頻率分布直方圖估計藥材![]() 的平均畝產量,若不考慮其他因素,試判斷2020年該村應種植藥材
的平均畝產量,若不考慮其他因素,試判斷2020年該村應種植藥材![]() 還是藥材
還是藥材![]() ?并說明理由.
?并說明理由.
參考公式: ,
,![]() (回歸方程
(回歸方程![]() 中)
中)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com