
【題目】科技創新能力是決定綜合國力和國際競爭力的關鍵因素,也是推動經濟實現高質量發展的重要支撐,而研發投入是科技創新的基本保障,下圖是某公司從2010年到2019年這10年研發投入的數據分布圖:

其中折線圖是該公司研發投入占當年總營收的百分比,條形圖是當年研發投入的數值(單位:十億元).
(I)從2010年至2019年中隨機選取一年,求該年研發投入占當年總營收的百分比超過10%的概率;
(II)從2010年至2019年中隨機選取兩個年份,設X表示其中研發投入超過500億元的年份的個數,求X的分布列和數學期望;
(III)根據圖中的信息,結合統計學知識,判斷該公司在發展的過程中是否比較重視研發,并說明理由.
【答案】(I)![]() ; (II)
; (II)![]() ,分布列如下:
,分布列如下:
| 0 | 1 | 2 |
|
|
|
|
(III)2010年到2019年共10年中,研發投入占當年總營收的百分比超過10%有9年,每年基本上都在增加,因此公司在發展的過程中重視研發.
【解析】
(I) 折線圖中2010年到2019年共10年中,2010年公司研發投入占當年總營收的百分比在![]() 以下
以下
(II) 2010年到2019年共10年中,研發投入超過500億元的有5年,![]() 的取值可能為0,1,2,超幾何分布求概率.
的取值可能為0,1,2,超幾何分布求概率.
(III) 圖中信息10年中,研發投入占當年總營收的百分比超過10%有9年,每年基本上都在增加, 判斷公司在發展的過程中比較重視研發.
(I)由題知,2010年到2019年共10年中,研發投入占當年總營收的百分比超過10%有9年,設從2010年至2019年中隨機選取一年,求該年研發投入占當年總營收的百分比超過10%為事件![]() ,
,![]() .
.
(II)由題意得![]() 的取值可能為0,1,2
的取值可能為0,1,2
![]() ,
,
![]() ,
,
![]() .
.
![]() 的分布列為
的分布列為
| 0 | 1 | 2 |
|
|
|
|
![]() .
.
(III)2010年到2019年共10年中,研發投入占當年總營收的百分比超過10%有9年,每年基本上都在增加,因此公司在發展的過程中重視研發.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站退出了關于生態文明建設進展情況的調查,調查數據表明,環境治理和保護問題仍是百姓最為關心的熱點,參與調查者中關注此問題的約占![]() .現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組
.現從參與關注生態文明建設的人群中隨機選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
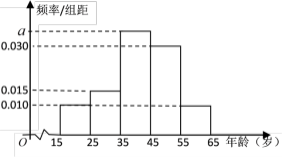
(I)求出![]() 的值;
的值;
(II)求出這200人年齡的樣本平均數(同一組數據用該區間的中點值作代表)和中位數(精確到小數點后一位);
(III)現在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機抽取3人進行問卷調查,求第2組恰好抽到2人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 、
、![]() 是
是![]() 上兩點.若
上兩點.若![]() ,且線段
,且線段![]() 的中點到
的中點到![]() 軸的距離等于
軸的距離等于![]() .
.
(1)求![]() 的值;
的值;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點且在
兩點且在![]() 軸的截距為負,過
軸的截距為負,過![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,若
,若![]() .
.
(i)證明:直線![]() 恒過定點,并求出該定點的坐標;
恒過定點,并求出該定點的坐標;
(ii)求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為實現國民經濟新“三步走”的發展戰略目標,國家加大了扶貧攻堅的力度,某地區在2015年以前的年均脫貧率(脫貧的戶數占當年貧困戶總數的比)為70%,2015年開始全面實施“精準扶貧”政策后,扶貧效果明顯提高,其中2019年度實施的扶貧項目,各項目參加戶數占比(參加戶數占2019年貧困總戶數的比)及該項目的脫貧率見下表:
實施項目 | 種植業 | 養殖業 | 工廠就業 |
參加占戶比 | 45% | 45% | 10% |
脫貧率 | 96% | 96% | 90% |
那么2019年的年脫貧率是實施“精準扶貧”政策前的年均脫貧率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右兩個焦點分別為
的左、右兩個焦點分別為![]() ,離心率
,離心率![]() ,短軸長為2.
,短軸長為2.
(1)求橢圓的方程;
(2)點![]() 為橢圓上的一動點(非長軸端點),
為橢圓上的一動點(非長軸端點),![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,
點, ![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,求
點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,如果存在區間
,如果存在區間![]() 滿足
滿足![]() 是
是![]() 上的單調函數,且
上的單調函數,且![]() 在區間
在區間![]() 上的值域也為
上的值域也為![]() ,則稱函數
,則稱函數![]() 為區間
為區間![]() 上的“保值函數”,
上的“保值函數”,![]() 為“保值區間”.根據此定義給出下列命題:①函數
為“保值區間”.根據此定義給出下列命題:①函數![]() 是
是![]() 上的“保值函數”;②若函數
上的“保值函數”;②若函數![]() 是
是![]() 上的“保值函數”,則
上的“保值函數”,則![]() ;③對于函數
;③對于函數![]() 存在區間
存在區間![]() ,且
,且![]() ,使函數
,使函數![]() 為
為![]() 上的“保值函數”.其中所有真命題的序號為( )
上的“保值函數”.其中所有真命題的序號為( )
A.②B.③C.①③D.②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國著名數學家華羅庚先生曾說:數缺形時少直觀,形缺數時難入微,數形結合百般好,隔裂分家萬事休.在數學的學習和研究中,常用函數的圖象研究函數的性質,也常用函數的解析式來琢磨函數的圖象特征.如函數![]() 的圖象大致為( )
的圖象大致為( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
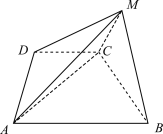
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)在棱![]() 上是否存在一點E,使得二面角
上是否存在一點E,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com