
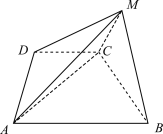
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)在棱![]() 上是否存在一點E,使得二面角
上是否存在一點E,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)證明見解析(2)證明見解析(3)存在;![]()
【解析】
(1)由線面平行判定定理證明即可;
(2)由勾股定理得出![]() ,進而得
,進而得![]() ,再由面面垂直的性質定理即可證明
,再由面面垂直的性質定理即可證明![]() 平面
平面![]() ;
;
(3)建立空間直角坐標系,利用向量法求解即可.
證明:(1)因為![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中點N,連接
的中點N,連接![]() .
.
在直角梯形![]() 中,
中,
易知![]() ,且
,且![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
在![]() 中,由勾股定理逆定理可知
中,由勾股定理逆定理可知![]() .
.
又因為平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
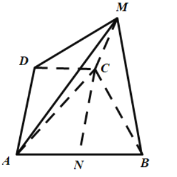
(3)取![]() 的中點O,連接
的中點O,連接![]() ,
,![]() .
.
所以![]() ,
,
因為![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因為![]() ,
,
所以![]() .
.
如圖建立空間直角坐標系![]() ,
,

則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
易知平面![]() 的一個法向量為
的一個法向量為![]() .
.
假設在棱![]() 上存在一點E,使得二面角
上存在一點E,使得二面角![]() 的大小為
的大小為![]() .
.
不妨設![]() (
(![]() ),
),
所以![]() ,
,
設![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
則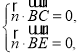 即
即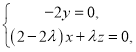
令![]() ,
,![]() ,所以
,所以![]() .
.
從而 .
.
解得![]() 或
或![]() .
.
因為![]() ,所以
,所以![]() .
.
由題知二面角![]() 為銳二面角.
為銳二面角.
所以在棱![]() 上存在一點E,使得二面角
上存在一點E,使得二面角![]() 的大小為
的大小為![]() ,
,
此時![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】科技創新能力是決定綜合國力和國際競爭力的關鍵因素,也是推動經濟實現高質量發展的重要支撐,而研發投入是科技創新的基本保障,下圖是某公司從2010年到2019年這10年研發投入的數據分布圖:

其中折線圖是該公司研發投入占當年總營收的百分比,條形圖是當年研發投入的數值(單位:十億元).
(I)從2010年至2019年中隨機選取一年,求該年研發投入占當年總營收的百分比超過10%的概率;
(II)從2010年至2019年中隨機選取兩個年份,設X表示其中研發投入超過500億元的年份的個數,求X的分布列和數學期望;
(III)根據圖中的信息,結合統計學知識,判斷該公司在發展的過程中是否比較重視研發,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國著名數學家華羅庚先生曾說:數缺形時少直觀,形缺數時難入微,數形結合百般好,隔裂分家萬事休.在數學的學習和研究中,常用函數的圖象研究函數的性質,也常用函數的解析式來琢磨函數的圖象特征.如函數![]() 的圖象大致為( )
的圖象大致為( )
A. B.
B.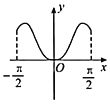
C.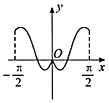 D.
D.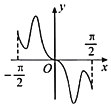
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)求函數![]() 的極值點;
的極值點;
(2)定義:若函數![]() 的圖像與直線
的圖像與直線![]() 有公共點,我們稱函數
有公共點,我們稱函數![]() 有不動點.這里取:
有不動點.這里取:![]() ,若
,若![]() ,如果函數
,如果函數![]() 存在不動點,求實數
存在不動點,求實數![]() 取值范圍.
取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 過點
過點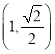 ,且橢圓的離心率為
,且橢圓的離心率為![]() ,直線
,直線![]() :
:![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中垂線交橢圓
的中垂線交橢圓![]() 于
于![]() 、
、![]() 兩點.
兩點.
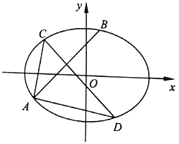
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求線段![]() 長的最大值;
長的最大值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(1),在矩形![]() 中,
中,![]() ,
,![]() 在邊
在邊![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 將
將![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都與平面
都與平面![]() 垂直,如圖(2).
垂直,如圖(2).
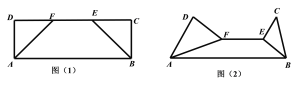
(1)試判斷圖(2)中直線![]() 與
與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)求平面![]() 和平面
和平面![]() 所成銳角二面角的余弦值.
所成銳角二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列四個結論:
,給出下列四個結論:
①函數![]() 的最小正周期是
的最小正周期是![]() ;
;
②函數![]() 在區間
在區間![]() 上是減函數;
上是減函數;
③函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
④函數![]() 的圖象可由函數
的圖象可由函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位得到其中所有正確結論的編號是( )
個單位得到其中所有正確結論的編號是( )
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:在長方體![]() 中,
中,![]() ,點
,點![]() 是線段
是線段![]() 上的一個動點,則①
上的一個動點,則①![]() 的最小值等于__________;②直線
的最小值等于__________;②直線![]() 與平面
與平面![]() 所成角的正切值的取值范圍為____________.
所成角的正切值的取值范圍為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com