
【題目】已知函數f(x)=1﹣ ![]() 在R上是奇函數.
在R上是奇函數.
(1)求a;
(2)對x∈(0,1],不等式sf(x)≥2x﹣1恒成立,求實數s的取值范圍;
(3)令g(x)= ![]() ,若關于x的方程g(2x)﹣mg(x+1)=0有唯一實數解,求實數m的取值范圍.
,若關于x的方程g(2x)﹣mg(x+1)=0有唯一實數解,求實數m的取值范圍.
【答案】
(1)解:由題意知f(0)=0.即 ![]() ,
,
所以a=2.此時f(x)= ![]() ,
,
而f(﹣x)= ![]() ,
,
所以f(x)為奇函數,故a=2為所求
(2)解:由(1)知 ![]() ,
,
因為x∈(0,1],所以2x﹣1>0,2x+1>0,
故sf(x)≥2x﹣1恒成立等價于s≥2x+1恒成立,
因為2x+1∈(2,3],所以只需s≥3即可使原不等式恒成立.
故s的取值范圍是[3,+∞)
(3)解:因為 ![]() .
.
所以g(2x)﹣mg(x+1)= ![]() .
.
整理得22x﹣2m2x﹣m+1=0.
令t=2x>0,則問題化為t2﹣2mt﹣m+1=0有一個正根或兩個相等正根.
令h(t)=t2﹣2mt﹣m+1(t>0),則函數h(t)=t2﹣2mt﹣m+1在(0,+∞)上有唯一零點.
所以h(0)≤0或 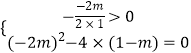 ,
,
由h(0)≤0得m≥1,
易知m=1時,h(t)=t2﹣2t符合題意;
由 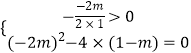 解得
解得 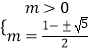 ,
,
所以m= ![]() .
.
綜上m的取值范圍是 ![]()
【解析】(1)根據f(0)=0可求得a的值,然后驗證a的取值滿足函數為奇函數;(2)分離參數法,將問題轉化為函數的最值問題求解;(3)可先將方程化簡,然后問題轉化為一元二次方程在指定區間上根的分布問題,然后再進一步求解.
【考點精析】本題主要考查了函數奇偶性的性質的相關知識點,需要掌握在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】將函數f(x)=2sin(2x+ ![]() )的圖象向右平移φ(φ>0)個單位,再將圖象上每一點橫坐標縮短到原來的
)的圖象向右平移φ(φ>0)個單位,再將圖象上每一點橫坐標縮短到原來的 ![]() 倍,所得圖象關于直線x=
倍,所得圖象關于直線x= ![]() 對稱,則φ的最小正值為 .
對稱,則φ的最小正值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱柱ABCD﹣A1B1C1D1中,側棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E為棱AA1的中點. 
(1)證明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)設點M在線段C1E上,且直線AM與平面ADD1A1所成角的正弦值為 ![]() ,求線段AM的長.
,求線段AM的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓心為C的圓過點A(0,﹣6)和B(1,﹣5),且圓心在直線l:x﹣y+1=0上.
(1)求圓心為C的圓的標準方程;
(2)過點M(2,8)作圓的切線,求切線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取某中學甲乙兩班各6名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖,則甲班樣本數據的眾數和乙班樣本數據的中位數分別是( ) 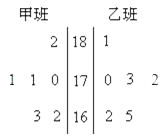
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)對于任意x∈R有 ![]() ,且當x∈[﹣1,1]時,f(x)=x2+1,則以下命題正確的是: ①函數數y=f(x)是周期為2的偶函數;
,且當x∈[﹣1,1]時,f(x)=x2+1,則以下命題正確的是: ①函數數y=f(x)是周期為2的偶函數;
②函數y=f(x)在[2,3]上單調遞增;
③函數 ![]() 的最大值是4;
的最大值是4;
④若關于x的方程[f(x)]2﹣f(x)﹣m=0有實根,則實數m的范圍是[0,2];
⑤當x1 , x2∈[1,3]時, ![]() .
.
其中真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)是定義在(0,+∞)上的函數,并且滿足下面三個條件: ①對任意正數x,y,都有f(xy)=f(x)+f(y);
②當x>1時,f(x)>0;
③f(3)=1,
(1)求f(1), ![]() 的值;
的值;
(2)判斷函數f(x)在區間(0,+∞)上單調性,并用定義給出證明;
(3)對于定義域內的任意實數x,f(kx)+f(4﹣x)<2(k為常數,且k>0)恒成立,求正實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1 , 底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分別是A1B1、A1A的中點. 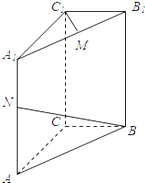
(1)求 ![]() 的長;
的長;
(2)求cos( ![]()
![]() )的值;
)的值;
(3)求證A1B⊥C1M.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com