【題目】已知拋物線
焦點為
，直線
過與拋物線交于
兩點.到準線的距離之和最小為8.
（1）求拋物線方程；
（2）若拋物線上一點
縱坐標為
，直線
分別交準線于
.求證：以
為直徑的圓過焦點.
【答案】（1）
（2）證明見解析
【解析】
（1）根據題意及拋物線定義，可知
，從而可求出拋物線方程；
（2）當直線
與
軸垂直時，求出
，
的坐標，進而證得以
為直徑的圓過焦點
；當直線與軸不垂直時，設出直線方程，
點和
點坐標，并與拋物線方程聯立，
借助根與系數的關系以及向量數量積的坐標表示，證得
，從而證出以為直徑的圓過焦點.
（1）
到準線的距離之和等于到焦點的距離之和，即為
，
最小為通徑，所以，解得
，
所以拋物線方程為.
（2）拋物線焦點
，準線方程：
，
由
點縱坐標為
，得
，
當直線與
軸垂直時，
直線方程為
，此時，
，
，
直線
：
，直線
：
，
所以，
，
，
所以，圓心坐標為
，半徑
，
焦點到圓心的距離
，
此時，以為直徑的圓過焦點.
當直線與軸不垂直時，
設直線
，設
，
，得
，
，
，
直線為
代入準線得：
同理可得
，
所以
，所以焦點在以為直徑的圓上.
綜上，以為直徑的圓過焦點.
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目：高中數學 來源： 題型：
【題目】某健身館為響應十九屆四中全會提出的“聚焦增強人民體質，健全促進全民健身制度性舉措”，提高廣大市民對全民健身運動的參與程度，推出了讓健身館會員參與的健身促銷活動．
（1）為了解會員對促銷活動的興趣程度，現從某周六參加該健身館健身活動的會員中隨機采訪男性會員和女性會員各
人，他們對于此次健身館健身促銷活動感興趣的程度如下表所示：
感興趣 | 無所謂 | 合計 | |
男性 |
|
|
|
女性 |
|
|
|
合計 |
|
|
|
根據以上數據能否有
的把握認為“對健身促銷活動感興趣”與“性別”有關？
（參考公式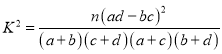
，其中
）
|
|
|
|
|
|
|
|
|
|
|
|
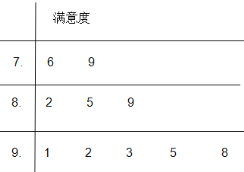
（2）在感興趣的會員中隨機抽取
人對此次健身促銷活動的滿意度進行調查，以莖葉圖記錄了他們對此次健身促銷活動滿意度的分數（滿分分），如圖所示，若將此莖葉圖中滿意度分為“很滿意”（分數不低于
分）、“滿意”（分數不低于平均分且低于分）、“基本滿意”（分數低于平均分）三個級別．先從“滿意”和“很滿意”的會員中隨機抽取兩人參加回訪饋贈活動，求這兩人中至少有一人是“很滿意”會員的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中，四邊形
，
均為正方形，且
，M為
的中點，N為
的中點．
（1）求證：
平面ABC；
（2）求二面角
的正弦值；
（3）設P是棱
上一點，若直線PM與平面
所成角的正弦值為
，求
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的最小正周期為
，將
的圖象向左平移
個單位后，所得圖象關于原點對稱，則函數的圖象（ ）
A.關于直線
對稱B.關于直線
對稱
C.關于點(
，0)對稱D.關于點(，0)對稱
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某科研單位到某大學的光電信息科學工程專業招聘暑期實習生，該專業一班30名同學全部報名，該科研單位對每個學生的測試是光電實驗，這30名學生測試成績的莖葉圖如圖所示.
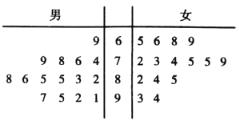
（1）求男同學測試成績的平均數及中位數；
（2）從80分以上的女同學中任意選取3人，求恰有2人成績位于
的概率；
（3）若80分及其以上定為優秀，80分以下定為合格，作出該班男女同學成績“優秀”、“合格”的
列聯表，并判斷是否有90%的把握認為該次測試是否優秀與性別有關？
附：
| 0.15 | 0.10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
.
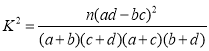查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《九章算術》中有一分鹿問題：“今有大夫、不更、簪裊、上造、公士，凡五人，共獵得五鹿.欲以爵次分之，問各得幾何.”在這個問題中，大夫、不更、簪裊、上造、公士是古代五個不同爵次的官員，現皇帝將大夫、不更、簪梟、上造、公士這5人分成兩組（一組2人，一組3人），派去兩地執行公務，則大夫、不更恰好在同一組的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
