【題目】設入射光線沿直線y=2x+1射向直線y=x，則被y=x反射后，反射光線所在的直線方程是（ ）
A.x﹣2y﹣1=0
B.x﹣2y+1=0
C.3x﹣2y+1=0
D.x+2y+3=0
科目：高中數學 來源： 題型：
【題目】函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ 
）（x∈R）的部分圖象如圖所示．
（Ⅰ）求函數f（x）的解析式并求函數f（x）的單調遞增區間；
（Ⅱ）求函數f（x）的最小值并指出函數f（x）取最小值時相應的x的值．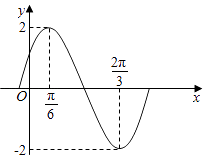
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知以點A（﹣1，2）為圓心的圓與直線m：x+2y+7=0相切，過點B（﹣2，0）的動直線l與圓A相交于M、N兩點
（1）求圓A的方程．
（2）當|MN|=2 
時，求直線l方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是定義在區間[﹣1，1]上的奇函數，且f（﹣1）=1，若m，n∈[﹣1，1]，m+n≠0時，有 
＜0．
（1）解不等式f（x+ 
）＜f（1﹣x）；
（2）若f（x）≤t2﹣2at+1對所有x∈[﹣1，1]，a∈[﹣1，1]恒成立，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知曲線
： 
（
為參數）和直線
： 
（
為參數）．
（1）將曲線
的方程化為普通方程；
（2）設直線
與曲線
交于
兩點，且
為弦
的中點，求弦
所在的直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xoy中，已知圓C1：（x+3）2+（y﹣1）2=4和圓C2：（x﹣4）2+（y﹣5）2=4
（1）若直線l過點A（4，0），且被圓C1截得的弦長為2 
，求直線l的方程
（2）設P為平面上的點，滿足：存在過點P的無窮多對互相垂直的直線l1和l2 ， 它們分別與圓C1和C2相交，且直線l1被圓C1截得的弦長與直線l2被圓C2截得的弦長相等，求所有滿足條件的點P的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（12分）
某超市計劃按月訂購一種酸奶，每天進貨量相同，進貨成本每瓶4元，售價每瓶6元，未售出的酸奶降價處理，以每瓶2元的價格當天全部處理完．根據往年銷售經驗，每天需求量與當天最高氣溫（單位：℃）有關．如果最高氣溫不低于25，需求量為500瓶；如果最高氣溫位于區間[20，25），需求量為300瓶；如果最高氣溫低于20，需求量為200瓶．為了確定六月份的訂購計劃，統計了前三年六月份各天的最高氣溫數據，得下面的頻數分布表：
最高氣溫 | [10，15） | [15，20） | [20，25） | [25，30） | [30，35） | [35，40） |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率。
（1）求六月份這種酸奶一天的需求量不超過300瓶的概率；
（2）設六月份一天銷售這種酸奶的利潤為Y（單位：元），當六月份這種酸奶一天的進貨量為450瓶時，寫出Y的所有可能值，并估計Y大于零的概率．學#科@網
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國歷法推測遵循以測為輔、以算為主的原則.例如《周髀算經》和《易經》里對二十四節氣的晷影長的記錄中，冬至和夏至的晷影長是實測得到的，其他節氣的晷影長則是按照等差數列的規律計算得出的.下表為《周髀算經》對二十四節氣晷影長的記錄，其中
寸表示115寸
分（1寸=10分）.
節氣 | 冬至 | 小寒（大雪） | 大寒（小雪） | 立春（立冬） | 雨水（霜降） | 驚蟄（寒露） | 春分（秋分） |
晷影長（寸） | 135 |
|
|
|
|
| 75.5 |
節氣 | 清明（白露） | 谷雨（處暑） | 立夏（立秋） | 小滿（大暑） | 芒種（小暑） | 夏至 | |
晷影長（寸） |
|
|
|
|
| 16.0 |
已知《易知》中記錄的冬至晷影長為130.0寸，夏至晷影長為14.8寸，那么《易經》中所記錄的驚蟄的晷影長應為__________寸．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
