
【題目】若數列![]() 滿足“對任意正整數
滿足“對任意正整數![]() ,都存在正整數
,都存在正整數![]() ,使得
,使得![]() ”,則稱數列
”,則稱數列![]() 具有“性質
具有“性質![]() ”.已知數列
”.已知數列![]() 為無窮數列.
為無窮數列.
(1)若![]() 為等比數列,且
為等比數列,且![]() ,判斷數列
,判斷數列![]() 是否具有“性質
是否具有“性質![]() ”,并說明理由;
”,并說明理由;
(2)若![]() 為等差數列,且公差
為等差數列,且公差![]() ,求證:數列
,求證:數列![]() 不具有“性質
不具有“性質![]() ”;
”;
(3)若等差數列![]() 具有“性質
具有“性質![]() ”,且
”,且![]() ,求數列
,求數列![]() 的通項公式
的通項公式![]() .
.
【答案】(1)數列![]() 具有“性質
具有“性質![]() ”.見解析(2)見解析(3)
”.見解析(2)見解析(3)![]()
【解析】
(1)由題可知,![]() 為等比數列,且
為等比數列,且![]() ,設數列
,設數列![]() 的公比為
的公比為![]() ,則
,則![]() ,
,![]() ,根據條件整理得出
,根據條件整理得出![]() ,所以數列
,所以數列![]() 具有“性質
具有“性質![]() ”;
”;
(2)由于![]() 為等差數列,且公差
為等差數列,且公差![]() ,則
,則![]() ,分類討論
,分類討論![]() 和
和![]() 時,都得出不存在正整數
時,都得出不存在正整數![]() ,使得
,使得![]() ,則當
,則當![]() 時,數列
時,數列![]() 不具有“性質
不具有“性質![]() ”;
”;
(3)已知等差數列![]() 具有“性質
具有“性質![]() ”,且
”,且![]() ,設數列
,設數列![]() 的公差為
的公差為![]() ,則
,則![]() ,且對任意
,且對任意![]() ,都存在正整數
,都存在正整數![]() ,使得
,使得![]() ,結合條件可求出
,結合條件可求出![]() 或
或![]() ,即可求出數列
,即可求出數列![]() 的通項公式
的通項公式![]() .
.
(1)解:數列![]() 具有“性質
具有“性質![]() ”.
”.
由題可知,![]() 為等比數列,且
為等比數列,且![]() ,
,
設數列![]() 的公比為
的公比為![]() ,則
,則![]() ,
,![]() ,
,
對任意正整數![]() ,
,![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,則
,則![]() ,
,
即對任意正整數![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,
所以數列![]() 具有“性質
具有“性質![]() ”.
”.
(2)證明:由于![]() 為等差數列,且公差
為等差數列,且公差![]() ,
,
則![]() ,
,
①若![]() ,則
,則![]() ,
,![]() ,
,
所以不存在正整數![]() ,使得
,使得![]() .
.
②若![]() ,則當
,則當![]() 時,
時,
![]() ,
,![]() ,
,
所以不存在正整數![]() ,使得
,使得![]() ;
;
綜上,當![]() 時,數列
時,數列![]() 不具有“性質
不具有“性質![]() ”.
”.
(3) 解:已知等差數列![]() 具有“性質
具有“性質![]() ”,且
”,且![]() ,
,
設數列![]() 的公差為
的公差為![]() ,則
,則![]() ,
,
由已知,對任意![]() ,都存在正整數
,都存在正整數![]() ,使得
,使得![]() ,
,
即![]() ,
,
所以![]() ,且
,且![]() ①
①
對任意![]() ,設
,設![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,得
,得![]() ,
,
因此![]() ②
②
由(2)知![]() ,
,
又由①、②可得![]() 或
或![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,不滿足要求,
,不滿足要求,
所以![]() ,
,![]() ,
,
可以驗證![]() 滿足要求.
滿足要求.


 優加精卷系列答案
優加精卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,連接
,連接![]() 和
和![]() .
.
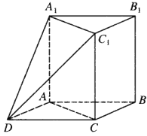
(1)求證:![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使平面
,使平面![]() 與平面
與平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與橢圓
與橢圓![]() 相交于點M(0,1),N(0,-1),且橢圓的離心率為
相交于點M(0,1),N(0,-1),且橢圓的離心率為![]() .
.

(1)求![]() 的值和橢圓C的方程;
的值和橢圓C的方程;
(2)過點M的直線![]() 交圓O和橢圓C分別于A,B兩點.
交圓O和橢圓C分別于A,B兩點.
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②設直線NA的斜率為![]() ,直線NB的斜率為
,直線NB的斜率為![]() ,問:
,問:![]() 是否為定值? 如果是,求出定值;如果不是,說明理由.
是否為定值? 如果是,求出定值;如果不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且與
且與![]() 軸垂直的直線被橢圓截得的線段長為
軸垂直的直線被橢圓截得的線段長為![]() ,且
,且![]() 與短軸兩端點的連線相互垂直.
與短軸兩端點的連線相互垂直.
(1)求橢圓![]() 的方程;
的方程;
(2)若圓![]() 上存在兩點
上存在兩點![]() ,
,![]() ,橢圓
,橢圓![]() 上存在兩個點
上存在兩個點![]() 滿足:
滿足:![]() 三點共線,
三點共線,![]() 三點共線,且
三點共線,且![]() ,求四邊形
,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為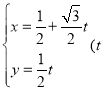 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車又稱為小黃車,近年來逐漸走進了人們的生活,也成為減少空氣污染,緩解城市交通壓力的一種重要手段.為調查某地區居民對共享單車的使用情況,從該地區居民中按年齡用隨機抽樣的方式隨機抽取了![]() 人進行問卷調查,得到這
人進行問卷調查,得到這![]() 人對共享單車的評價得分統計填入莖葉圖,如下所示(滿分
人對共享單車的評價得分統計填入莖葉圖,如下所示(滿分![]() 分):
分):

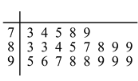
(1)找出居民問卷得分的眾數和中位數;
(2)請計算這![]() 位居民問卷的平均得分;
位居民問卷的平均得分;
(3)若在成績為![]() 分的居民中隨機抽取
分的居民中隨機抽取![]() 人,求恰有
人,求恰有![]() 人成績超過
人成績超過![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇跡之一,其中較為著名的是胡夫金字塔.令人吃驚的并不僅僅是胡夫金字塔的雄壯身姿,還有發生在胡夫金字塔上的數字“巧合”.如胡夫金字塔的底部周長如果除以其高度的兩倍,得到的商為3.14159,這就是圓周率較為精確的近似值.金字塔底部形為正方形,整個塔形為正四棱錐,經古代能工巧匠建設完成后,底座邊長大約230米.因年久風化,頂端剝落10米,則胡夫金字塔現高大約為( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點是橢圓
的頂點是橢圓![]() 的中心,焦點與該橢圓的右焦點重合.
的中心,焦點與該橢圓的右焦點重合.
(1)求拋物線![]() 的方程;
的方程;
(2)已知動直線![]() 過點
過點![]() ,交拋物線
,交拋物線![]() 于
于![]() ,
,![]() 兩點,坐標原點
兩點,坐標原點![]() 為
為![]() 的中點,求證
的中點,求證![]() ;
;
(3)在(2)的條件下,是否存在垂直于![]() 軸的直線
軸的直線![]() 被以
被以![]() 為直徑的圓所截得的弦長恒為定值?如果存在,求出
為直徑的圓所截得的弦長恒為定值?如果存在,求出![]() 的方程;如果不存在,請說明理由.
的方程;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com