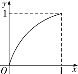
【題目】已知定義在區間[0,1]上的函數y＝f(x)的圖象如圖所示．對滿足0<x1<x2<1的任意x1，x2，給出下列結論：
①f(x1)－f(x2)>x1－x2；
②f(x1)－f(x2)<x1－x2；
③x2f(x1)>x1f(x2)；
④
．
其中正確結論的序號是________．
【答案】③④
【解析】
根據題意可作出函數
的圖象，根據直線的斜率的幾何意義，利用數形結合的思想
研究函數的單調性與最值即可得到結論.
由于k＝
表示函數圖象上兩點(x1，f(x1))，(x2，f(x2))連線的斜率，當x1和x2都接近于零時，由圖象可知k>1，
當x1和x2都接近于1時，k<1，
故①②均不正確；
當0＜x1＜x2＜1時，根據斜率關系有
>
，
即x2f(x1)＞x1f(x2)，所以③正確；
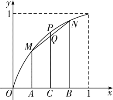
在區間(0,1)上任取兩點A、B，其橫坐標分別為x1，x2，過A、B分別作x軸的垂線，
與曲線交于點M、N，取AB中點C，過C作x軸的垂線，
與曲線交點為P，與線段MN交點為Q，
則
＝CQ，f(
)＝CP，
由圖象易知CP>CQ，
故有＜f()，所以④正確．故答案為③④.
科目：高中數學 來源： 題型：
【題目】2019年底，北京2022年冬奧組委會啟動志愿者全球招募，僅一個月內報名人數便突破60萬，其中青年學生約有50萬人.現從這50萬青年學生志愿者中，按男女分層抽樣隨機選取20人進行英語水平測試，所得成績(單位:分)統計結果用莖葉圖記錄如下:
(Ⅰ)試估計在這50萬青年學生志愿者中，英語測試成績在80分以上的女生人數;
(Ⅱ)從選出的8名男生中隨機抽取2人，記其中測試成績在70分以上的人數為X，求
的分布列和數學期望;
(Ⅲ)為便于聯絡，現將所有的青年學生志愿者隨機分成若干組(每組人數不少于5000)，并在每組中隨機選取
個人作為聯絡員，要求每組的聯絡員中至少有1人的英語測試成績在70分以上的概率大于90%.根據圖表中數據，以頻率作為概率，給出的最小值.(結論不要求證明)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一次考試結束后，隨機抽查了某校高三（1）班5名同學的數學與物理成績如下表：
學生 |
|
|
|
|
|
數學 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
（Ⅰ）分別求這5名同學數學與物理成績的平均分與方差，并估計該班數學與物理成績那科更穩定；
（Ⅱ）從以上5名同學中選2人參加一項活動，求選中的學生中至少有一個物理成績高于90分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）若曲線
在
處的切線與
軸平行，求
；
（2）已知
在
上的最大值不小于
，求的取值范圍；
（3）寫出所有可能的零點個數及相應的的取值范圍.（請直接寫出結論）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知甲盒內有大小相同的1個紅球和3個黑球，乙盒內有大小相同的3個紅球和3個黑球，現從甲、乙兩個盒內各任取2個球。
（1）求取出的4個球中沒有紅球的概率；
（2）求取出的4個球中恰有1個紅球的概率；
（3）設
為取出的4個球中紅球的個數，求
的分布列和數學期望。
查看答案和解析>>
科目：高中數學 來源： 題型：
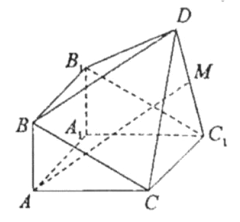
【題目】如圖，由直三棱柱
和四棱錐
構成的幾何體中，
，平面
平面
（I）求證：
；
（II）若M為
中點，求證：
平面
；
（III）在線段BC上（含端點）是否存在點P，使直線DP與平面所成的角為
？若存在，求
得值，若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
