
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)設定義在![]() 上的函數
上的函數![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,且
,且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,以極軸為
,以極點為原點,以極軸為![]() 軸的正半軸,取相同的單位長度,建立平面直角坐標系,直線
軸的正半軸,取相同的單位長度,建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為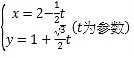 .
.
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 經過伸縮變換
經過伸縮變換![]() 得到曲線
得到曲線![]() ,曲線
,曲線![]() 上任一點為
上任一點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”,為了響應國家政策,我市環保部門對市民進行了一次環境保護知識的網絡問卷調查,每位市民僅有一次參加機會,通過隨機抽樣,得到參與問卷調查的50人的得分(滿分:100分)數據,統計結果如表所示:
組別 |
|
|
|
|
|
|
男 | 1 | 2 | 2 | 10 | 9 | 6 |
女 | 0 | 5 | 5 | 5 | 3 | 2 |
若規定問卷得分不低于70分的市民稱為“環境保護關注者”,則上圖中表格可得![]() 列聯表如下:
列聯表如下:
非“環境保護關注者” | 是“環境保護關注者” | 合計 | |
男 | 5 | 25 | 30 |
女 | 10 | 10 | 20 |
合計 | 15 | 35 | 50 |
(1)請完成上述![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關?
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“環境保護關注者”與性別有關?
(2)若問卷得分不低于80分的人稱為“環境保護達人”,現在從本次調查的“環境保護達人”中利用分層抽樣的方法抽取4名市民參與環保知識問答,再從這4名市民中隨機抽取2人參與座談會,求抽取的2名市民中,既有男“環境保護達人”又有女“環境保護達人”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】推進垃圾分類處理,是落實綠色發展理念的必然選擇,也是打贏污染防治攻堅戰的重要環節.為了解居民對垃圾分類的了解程度,某社區居委會隨機抽取1000名社區居民參與問卷測試,并將問卷得分繪制頻率分布表如下:
得分 |
|
|
|
|
|
|
|
男性人數 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人數 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)從該社區隨機抽取一名居民參與問卷測試,試估計其得分不低于60分的概率;
(2)將居民對垃圾分類的了解程度分為“比較了解“(得分不低于60分)和“不太了解”(得分低于60分)兩類,完成![]() 列聯表,并判斷是否有95%的把握認為“居民對垃圾分類的了解程度”與“性別”有關?
列聯表,并判斷是否有95%的把握認為“居民對垃圾分類的了解程度”與“性別”有關?
不太了解 | 比較了解 | |
男性 | ||
女性 |
(3)從參與問卷測試且得分不低于80分的居民中,按照性別進行分層抽樣,共抽取10人,連同![]() 名男性調查員一起組成3個環保宜傳隊.若從這
名男性調查員一起組成3個環保宜傳隊.若從這![]() 中隨機抽取3人作為隊長,且男性隊長人數占的期望不小于2.求
中隨機抽取3人作為隊長,且男性隊長人數占的期望不小于2.求![]() 的最小值.
的最小值.
附:![]()
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從廣安市某中學校的![]() 名男生中隨機抽取
名男生中隨機抽取![]() 名測量身高,被測學生身高全部介于
名測量身高,被測學生身高全部介于![]() cm和
cm和![]() cm之間,將測量結果按如下方式分成八組:第一組
cm之間,將測量結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,...,第八組
,...,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為
,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為![]() 人.
人.
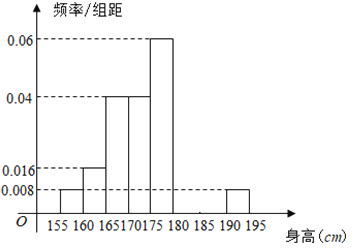
(1)求第七組的頻率;
(2)估計該校![]() 名男生的身高的中位數。
名男生的身高的中位數。
(3)若從樣本中身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,求抽出的兩名男生是同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在等腰梯形![]() 中,兩腰
中,兩腰![]() ,底邊
,底邊![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的三等分點,
的三等分點,![]() 是
是![]() 的中點.分別沿
的中點.分別沿![]() ,
,![]() 將四邊形
將四邊形![]() 和
和![]() 折起,使
折起,使![]() ,
,![]() 重合于點
重合于點![]() ,得到如圖2所示的幾何體.在圖2中,
,得到如圖2所示的幾何體.在圖2中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
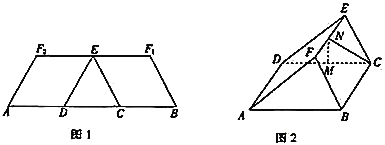
(1)證明:![]() 平面
平面![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有3名醫生,5名護士、2名麻醉師.
(1)從中選派1名去參加外出學習,有多少種不同的選法?
(2)從這些人中選出1名醫生、1名護士和1名麻醉師組成1個醫療小組,有多少種不同的選法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在區間[0,1]上的函數y=f(x)的圖象如圖所示.對滿足0<x1<x2<1的任意x1,x2,給出下列結論:
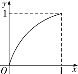
①f(x1)-f(x2)>x1-x2;
②f(x1)-f(x2)<x1-x2;
③x2f(x1)>x1f(x2);
④![]() .
.
其中正確結論的序號是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com