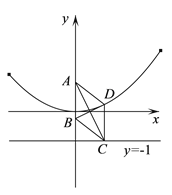
【題目】已知菱形
，
在
軸上且
，
（
，
）．
（Ⅰ）求
點軌跡
的方程；
（Ⅱ）延長
交軌跡于點
，軌跡在點處的切線與直線
交于點
，試判斷以為圓心，線段
為半徑的圓與直線的位置關系，并證明你的結論．
【答案】(Ⅰ)
（
）；(Ⅱ)答案見解析.
【解析】試題分析：
（Ⅰ）由題意可知對角線
與
垂直平分，由題意結合垂直平分線的性質可得點
到直線
的距離與到
點的距離相等，結合幾何關系可知
點軌跡方程為（）.
（Ⅱ）設
，
，聯立直線AD是方程與拋物線方程可得
,由題意結合韋達定理可得
，
，
，利用導數研究切線方程可得在點
處的切線方程為：
，且直線的方程為
，據此可得交點坐標
，即
，計算可得點
到直線
的距離
，則圓與直線相切.
試題解析：
（Ⅰ）因為
是菱形，所以對角線與垂直平分，
因為
在
軸上，所以
與直線垂直，
所以點到直線的距離與到點的距離相等，
所以點軌跡
為拋物線（不包含頂點），
其軌跡方程為（）.
（Ⅱ）設
，
，
設直線的方程為
，聯立可得：
所以
，
．
因為菱形，所以
，所以
，
所以，所以，
所以
，所以
由
可得
所以在點處的切線方程的斜率為
則切線的方程為：
，即……①
因為
，
，所以
，
又中點
，所以直線的方程為
②
聯立①②可得
，即點
，又，所以
所以
，點到直線的距離
所以圓與直線相切.
海淀課時新作業金榜卷系列答案
期末金牌卷系列答案
輕松課堂標準練系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）是定義域為R上的奇函數，當x＞0時，f（x）=x2+2x．
（1）求f（x）的解析式；
（2）若不等式f（t﹣2）+f（2t+1）＞0成立，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
對任意實數x、y恒有
，當x>0時，f(x)<0，且
.
(1)判斷的奇偶性；
(2)求在區間[-3,3]上的最大值；
(3)若
對所有的
恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
，
.
(1)當
時，若對任意
均有
成立，求實數
的取值范圍；
(2)設直線
與曲線
和曲線
相切，切點分別為
，
，其中
.
①求證：
；
②當
時，關于
的不等式
恒成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若質地均勻的六面體玩具各面分別標有數字1,2,3,4,5,6．拋擲該玩具后，任何一個數字所在的面朝上的概率均相等．拋擲該玩具一次，記事件A=“向上的面標記的數字是完全平方數（即能寫出整數的平方形式的數，如9=32,9是完全平方數）”
（1）甲、乙二人利用該玩具進行游戲，并規定：①甲拋擲一次，若事件A發生，則向上一面的點數的6倍為甲的得分；若事件A不發生，則甲得0分；②乙拋擲一次，將向上的一面對應的數字作為乙的得分。現甲、乙二人各拋擲該玩具一次，分別求二人得分的期望；
（2）拋擲該玩具一次，記事件B=“向上一面的點數不超過
”，若事件A與B相互獨立，試求出所有的整數
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某良種培育基地正在培育一種小麥新品種A，將其與原有的一個優良品種B進行對照試驗，兩種小麥各種植了24畝，所得畝產數據（單位：千克）如下：
品種A:357，359，367，368，375，388，392，399，400，405，412，414，415，421，423，423，427，430，430，434，443，445，451，454
品種B：363，371，374，383，385，386，391，392，394，395，397，397，400，401，401，403，406，407，410，412，415，416，422，430
（1）畫出莖葉圖.
（2）用莖葉圖處理現有的數據，有什么優點？
（3）通過觀察莖葉圖，對品種A與B的畝產量及其穩定性進行比較，寫出統計結論。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體QPABCD為一簡單組合體，在底面ABCD中，∠DAB＝60°，AD⊥DC，AB⊥BC，QD⊥平面ABCD，PA∥QD，PA＝1，AD＝AB＝QD＝2.
(1)求證：平面PAB⊥平面QBC；
(2)求該組合體QPABCD的體積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
