【題目】從裝有n+1個球（其中n個白球，1個黑球）的口袋中取出m個球（0＜m≤n，m，n∈N），共有 
種取法．在這 種取法中，可以分成兩類：一類是取出的m個球全部為白球，共有 
種取法；另一類是取出的m個球有m﹣1個白球和1個黑球，共有 
種取法．顯然 
，即有等式： 
成立．試根據上述思想化簡下列式子： 
= ．
【答案】Cn+km
【解析】解：在Cnm+Ck1Cnm﹣1+Ck2Cnm﹣2+…+CkkCnm﹣k中，
從第一項到最后一項分別表示：
從裝有n個白球，k個黑球的袋子里，
取出m個球的所有情況取法總數的和，
故答案應為：從從裝有n+k球中取出m個球的不同取法數Cn+km
故答案為：Cn+km．
從裝有n+1個球（其中n個白球，1個黑球）的口袋中取出m個球（0＜m≤n，m，n∈N），共有Cn+1m種取法．在這Cn+1m種取法中，可以分成兩類：一類是取出的m個球全部為白球，另一類是，取出1個黑球，m﹣1個白球，則Cnm+Cnm﹣1=Cn+1m根據上述思想，在式子：Cnm+Ck1Cnm﹣1+Ck2Cnm﹣2+…+CkkCnm﹣k中，從第一項到最后一項分別表示：從裝有n個白球，k個黑球的袋子里，取出m個球的所有情況取法總數的和，故答案應為：從從裝有n+k球中取出m個球的不同取法數，根據排列組合公式，易得答案．
科目：高中數學 來源： 題型：
【題目】某學校課題組為了研究學生的數學成績與學生細心程度的關系，在本校隨機調查了100名學生進行研究．研究結果表明：在數學成績及格的60名學生中有45人比較細心，另15人比較粗心；在數學成績不及格的40名學生中有10人比較細心，另30人比較粗心．
（1）試根據上述數據完成2×2列聯表；
數學成績及格 | 數學成績不及格 | 合計 | |
比較細心 | |||
比較粗心 | |||
合計 |
（2）能否在犯錯誤的概率不超過0.001的前提下認為學生的數學成績與細心程度有關系． 參考數據：獨立檢驗隨機變量K2的臨界值參考表：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（其中n=a+b+c+d）
查看答案和解析>>
科目：高中數學 來源： 題型：
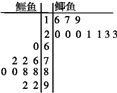
【題目】已知某池塘養殖著鯉魚和鯽魚,為了估計這兩種魚的數量,養殖者從池塘中捕出這兩種魚各1 000條,給每條魚做上不影響其存活的標記,然后放回池塘,待完全混合后,再每次從池塘中隨機地捕出1 000條魚,記錄下其中有記號的魚的數目,立即放回池塘中.這樣的記錄做了10次,并將記錄獲取的數據制作成如圖所示的莖葉圖.
(1)根據莖葉圖計算有記號的鯉魚和鯽魚數目的平均數,并估計池塘中的鯉魚和鯽魚的數量;
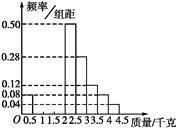
(2)為了估計池塘中魚的總質量,現按照(1)中的比例對100條魚進行稱重,根據稱重魚的質量介于[0,4.5](單位:千克)之間,將測量結果按如下方式分成九組:第一組[0,0.5),第二組[0.5,1),…,第九組[4,4.5].如圖是按上述分組方法得到的頻率分布直方圖的一部分.
①估計池塘中魚的質量在3千克以上(含3千克)的條數;
②若第三組魚的條數比第二組多7條、第四組魚的條數比第三組多7條,請將頻率分布直方圖補充完整;
③在②的條件下估計池塘中魚的質量的眾數及池塘中魚的總質量.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下面是60名男生每分鐘脈搏跳動次數的頻率分布表.
分組 | 頻數 | 頻率 |
|
[51.5,57.5) | 4 | 0.067 | 0.011 |
[57.5,63.5) | 6 | 0.1 | 0.017 |
[63.5,69.5) | 11 | 0.183 | 0.031 |
[69.5,75.5) | 20 | 0.333 | 0.056 |
[75.5,81.5) | 11 | 0.183 | 0.031 |
[81.5,87.5) | 5 | 0.083 | 0.014 |
[87.5,93.5] | 3 | 0.05 | 0.008 |
(1)作出其頻率分布直方圖;
(2)根據直方圖的各組中值估計總體平均數;
(3)估計每分鐘脈搏跳動次數的范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，PD⊥平面ABCD，AD∥BC，CD=13，AB=12，BC=10，AD=5，PD=8，點E，F分別是PB，DC的中點． 
（1）求證：EF∥平面PAD；
（2）求EF與平面PDB所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人各射擊一次，擊中目標的概率分別是 
和 
．假設兩人射擊是否擊中目標相互之間沒有影響；每人各次射擊是否擊中目標相互之間也沒有影響．
（1）求甲射擊4次，至少有1次未擊中目標的概率；
（2）求兩人各射擊4次，甲恰好擊中目標2次且乙恰好擊中目標3次的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax﹣lnx﹣a（a∈R）．
（1）討論函數f（x）的單調性；
（2）若a∈（0，+∞），x∈（1，+∞），證明：f（x）＜axlnx．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
