【題目】下列判斷中正確的是（ ）
A. “若
，則
有實數根”的逆否命題是假命題
B. “
”是“直線
與直線
平行”的充要條件
C. 命題“
”是真命題
D. 命題“
”在
時是假命題
【答案】D
【解析】
分別對四個選項進行判斷：A原命題與逆否命題同真同假，只需要判斷原命題真假或者寫出逆否命題判斷真假；B根據兩直線平行的條件
可解得
的值，然后判斷
是直線平行的什么條件；C先用三角函數輔助角公式化解，再對全稱命題判斷真假；D利用二次函數判別式小于0判斷t的范圍，然后判斷其真假.
A：原命題“若
，則
有實數根”的逆否命題為“若沒有實數根，則
”.
∵方程無實數根，
∴
,
因此“若沒有實數根，則”為真.
B： 若
，則兩條直線分別是
和
,顯然平行. 因此“”是“直線
與直線
平行”的充分條件.
反之，若“直線與直線平行”，則由
=
≠
，得
但當
時，兩直線分別是
也平行, 滿足題意. 因此“”是“直線與直線平行”的不必要條件.
綜上可知，“”是“直線與直線平行”的充分不必要條件.
C：因為
，所以命題“
”是假命題. D：當
即
是假命題.
故選D.
應用題天天練四川大學出版社系列答案科目：高中數學 來源： 題型：
【題目】[2019·吉林期末]一個袋中裝有6個大小形狀完全相同的球，球的編號分別為1，2，3，4，5，6．
（1）從袋中隨機抽取兩個球，求取出的球的編號之和為6的概率；
（2）先后有放回地隨機抽取兩個球，兩次取的球的編號分別記為
和
，求
的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}滿足：a3＝7，a5+a7＝26，{an}的前n項和為Sn．
（1）求an及Sn；
（2）令bn＝
（n∈N*），求數列{bn}的前n項和Tn．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2016年“雙節”期間，高速公路車輛較多．某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查，將他們在某段高速公路的車速
分成六段： 
， 
， 
， 
， 
， 
后得到如圖的頻率分布直方圖．
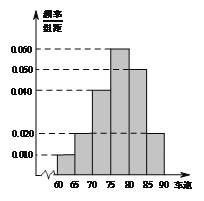
（I）某調查公司在采樣中，用到的是什么抽樣方法？
（II）求這40輛小型車輛車速的眾數、中位數及平均數的估計值；
(III)若從車速在
的車輛中任抽取2輛，求車速在
的車輛至少有一輛的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為進行“陽光運動一小時”活動，計劃在一塊直角三角形
的空地上修建一個占地面積為
（平方米）的矩形
健身場地。如圖，點
在
上，點
在
上，且
點在斜邊
上，已知
米，
米，
，設矩形健身場地每平方米的造價為
元，再把矩形以外（陰影部分）鋪上草坪，每平方米的造價為
元（
為正的常數）.
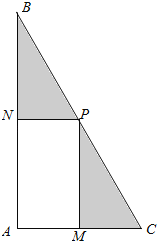
（1）試用
表示，并指出如何設計矩形的長和寬，才能使得矩形的面積最大，且求出的最大值；
（2）求總造價
關于面積的函數
，說明如何選取
，使總造價最低（不要求求出最低造價）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高中年級開設了豐富多彩的校本課程，甲、乙兩班各隨機抽取了5名學生的學分，用莖葉圖表示.
，
分別表示甲、乙兩班各自5名學生學分的標準差，則_______.（填“
”“<”或“＝”）
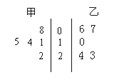
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，直平行六面體
中，
為棱
上任意一點，
為底面
（除
外）上一點，已知在底面
上的射影為
，若再增加一個條件，就能得到
，現給出以下條件：
①
；②在
上；③
平面
；④直線
和
在平面的射影為同一條直線．其中一定能成為增加條件的是__________．（把你認為正確的都填上）
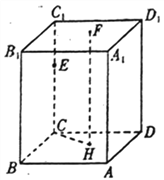
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在
中， 
， 
， 
， 
是
中點（如圖1）.將
沿
折起到圖2中
的位置，得到四棱錐
.
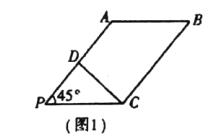
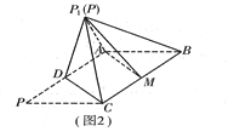
（1）將
沿
折起的過程中， 
平面
是否成立？并證明你的結論；
（2）若
，過
的平面交
于點
，且
為
的中點，求三棱錐
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
