【題目】已知
，函數
有兩個不同的極值點
，
．
（1）求
的取值范圍；
（2）證明：
．
【答案】（1）
；（2）見解析
【解析】
（1）求函數
的定義域
，以及導數
，將問題轉化為導數方程
，轉化為二次方程
在上有兩個不等的實根，再分析
、對稱軸以及二次函數
在
處函數值的正負，列出有關
的不等式組解出即可；
（2）由
、
為二次方程的兩根，列出韋達定理，再將韋達定理代入代數式
，經過化簡得出關于的函數，并令
，
轉化為關于
的函數，再利用導數結合單調性證明結論成立。
（1）
，函數
定義域：
．，
，
函數
有兩個不同的極值點，img src="http://thumb.zyjl.cn/questionBank/Upload/2020/05/28/06/0c1e6116/SYS202005280601105383817422_DA/SYS202005280601105383817422_DA.012.png" width="18" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />．對于
中的
應滿足①②③三個條件：
，①，△
，②
，③
由①②③可得的取值范圍：，
（2）證明：
，
得：
，．
，
，
令，則
，
將其令為
即：
，則有：
，
，
，
在定義域是單調遞減的函數，
（4）
，
在定義域也是單調遞減的函數，
（4）
．
即：
得證．
發散思維新課堂系列答案科目：高中數學 來源： 題型：
【題目】共有編號分別為1，2，3，4，5的五個座位，在甲同學不坐2號座位，乙同學不坐5號座位的條件下，甲、乙兩位同學的座位號相加是偶數的概率為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區甲、乙、丙三所單位進行招聘，其中甲單位招聘2名，乙單位招聘2名，丙單位招聘1名，并且甲單位要至少招聘一名男生，現有3男3女參加三所單位的招聘，則不同的錄取方案種數為（ ）
A.36B.72C.108D.144
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】窗花是貼在窗紙或窗戶玻璃上的剪紙，是中國古老的傳統民間藝術之一．圖中的窗花是由一張圓形紙片剪去一個正十字形剩下的部分，正十字形的頂點都在圓周上．已知正十字形的寬和長都分別為x，y（單位：dm）且x＜y，若剪去的正十字形部分面積為4dm2．
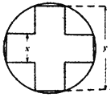
（1）求y關于x的函數解析式，并求其定義域；
（2）現為了節約紙張，需要所用圓形紙片面積最小．當x取何值時，所用到的圓形紙片面積最小，并求出其最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某企業的某種產品中抽取
件，測量這些產品的一項質量指標值，由測量結果得如下頻率分布直方圖：
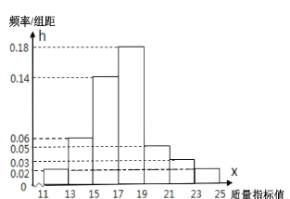
（Ⅰ）求這件產品質量指標值的樣本平均數
和樣本方差
（同一組數據用該區間的中點值作代表，記作
，
）；
（Ⅱ）由頻率分布直方圖可以認為，這種產品的質量指標值
服從正態分布
，其中
近似為樣本平均數，
近似為樣本方差．
（i）若使
的產品的質量指標值高于企業制定的合格標準，則合格標準的質量指標值大約為多少？
（ii）若該企業又生產了這種產品
件，且每件產品相互獨立，則這件產品質量指標值不低于
的件數最有可能是多少？
附：參考數據與公式：
，
；若
，則①
；②
；③
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小學對五年級的學生進行體質測試，已知五年一班共有學生30人，測試立定跳遠的成績用莖葉圖表示如圖（單位：
）：男生成績在175以上（包括175）定義為“合格”，成績在175以下（不包括175）定義為“不合格”．女生成績在165以上（包括165）定義為“合格”，成績在165以下（不包括165）定義為“不合格”．
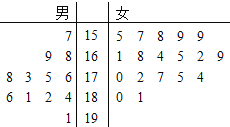
(1)求五年一班的女生立定跳遠成績的中位數；
(2)在五年一班的男生中任意選取3人，求至少有2人的成績是合格的概率；
(3)若從五年一班成績“合格”的學生中選取2人參加復試，用
表示其中男生的人數，寫出的分布列，并求的數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
